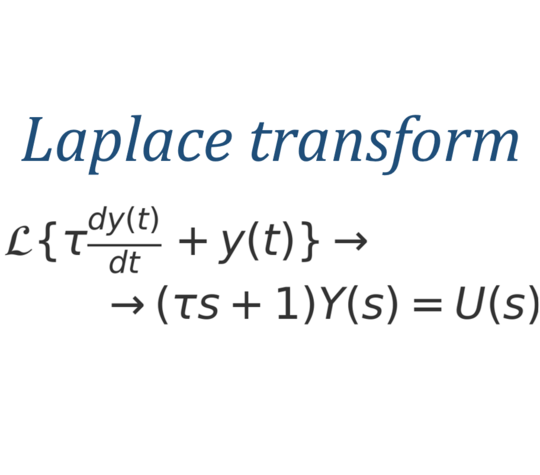Störungsanalyse der Mischgüte mit Laplace-Transformation
Beispielhafte Anwendung der Laplace-Transformation für einen kontinuierlichen Mischprozess im amixon®-Mischer AMK 1000: Pulver A strömt konstant mit 1.000 kg/h in den Mischer. Pulver B wird gleichzeitig mit 10 kg/h dosiert. Der Mischraum bleibt zu Beginn geschlossen. Das Mischwerkzeug läuft bereits und erreicht nach 20 Umdrehungen eine ideale Mischgüte. Es dreht mit 20 U/min.
Sobald im Mischer 700 kg Produkt vorhanden sind, öffnet sich die Austragsarmatur. Der Abfluss wird so eingestellt, dass die eingehenden 1.010 kg/h auch wieder ausgetragen werden. Der Prozess läuft stabil.
Plötzlich tritt eine Störung auf: Die Zufuhr von Komponente B stoppt für 20 Sekunden vollständig. Danach wird der Dosierer korrigiert und B strömt für 20 Sekunden mit doppelter Menge (20 kg/h). Anschließend stabilisiert sich der Zufluss wieder auf 10 kg/h.
Vor der Störung lag eine technisch ideale Mischgüte vor. Der Variationskoeffizient der Mischgüte betrug 3 %.
Prozess in Zahlen (Ausgangslage)
Zulauf A: ṁ_A = 1000 kg/h; Zulauf B (nominal): ṁ_B = 10 kg/h; Gesamtzulauf: ṁ_ein = 1010 kg/h. Konstante Pulvermasse im Mischer: M = 700 kg.
Mittlere Verweilzeit τ (Zeitkonstante):
τ = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s
Nominaler Massenanteil von B am Zulauf (und stationär am Auslauf):
x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)
Zulauf A: ṁ_A = 1000 kg/h; Zulauf B (nominal): ṁ_B = 10 kg/h; Gesamtzulauf: ṁ_ein = 1010 kg/h. Konstante Pulvermasse im Mischer: M = 700 kg.
Mittlere Verweilzeit τ (Zeitkonstante):
τ = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s
Nominaler Massenanteil von B am Zulauf (und stationär am Auslauf):
x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)
Störszenario (Zulauf B)
0 ≤ t < 20 s: Blockade, ṁ_B = 0; 20 ≤ t < 40 s:
Korrektur, ṁ_B = 20 kg/h; t ≥ 40 s: wieder 10 kg/h.
Wir betrachten die Abweichung des B-Anteils im Zulauf relativ zur Nennfraktion:
u(t) = x_B,in(t) − x_B,in,0.
Stückweise Definition (Totalsstrom näherungsweise konstant 1010 kg/h):
u(t) = {-x_B,in,0 für 0≤t<20 s; +x_B,in,0 für 20≤t<40 s; 0 für t≥40 s}
0 ≤ t < 20 s: Blockade, ṁ_B = 0; 20 ≤ t < 40 s:
Korrektur, ṁ_B = 20 kg/h; t ≥ 40 s: wieder 10 kg/h.
Wir betrachten die Abweichung des B-Anteils im Zulauf relativ zur Nennfraktion:
u(t) = x_B,in(t) − x_B,in,0.
Stückweise Definition (Totalsstrom näherungsweise konstant 1010 kg/h):
u(t) = {-x_B,in,0 für 0≤t<20 s; +x_B,in,0 für 20≤t<40 s; 0 für t≥40 s}
Dynamisches Modell (PT1, ideal durchmischt)
Laplace-Lösung
Laplace-Transformierte des PT1:
Y(s) = (1 / (τ s + 1)) · U(s)
τ (Tau): die Zeitkonstante des Systems (hier: die mittlere Verweilzeit im Mischer)
s: die Laplace-Variable, ein Maß dafür, wie sich Signale in der Zeit ändern
„τ · s“ ist eine dimensionslose Kombination aus Zeitkonstante und Änderungsrate.
Eingang u(t) als Differenz zweier Rechtecksprünge; mit Heaviside-Verschiebungen ergibt sich:
U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s
Zeitbereichslösung (Überlagerung von Schrittantworten, Heaviside H(·)):
y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]
Laplace-Transformierte des PT1:
Y(s) = (1 / (τ s + 1)) · U(s)
τ (Tau): die Zeitkonstante des Systems (hier: die mittlere Verweilzeit im Mischer)
s: die Laplace-Variable, ein Maß dafür, wie sich Signale in der Zeit ändern
„τ · s“ ist eine dimensionslose Kombination aus Zeitkonstante und Änderungsrate.
Eingang u(t) als Differenz zweier Rechtecksprünge; mit Heaviside-Verschiebungen ergibt sich:
U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s
Zeitbereichslösung (Überlagerung von Schrittantworten, Heaviside H(·)):
y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]
Zahlenwerte und Maximalabweichung
Mit τ = 2495 s und x_B,in,0 = 0,00990099 ergeben sich:
e^{-20/τ} = e^{-20/2495} ≈ 0,99202; 1 - e^{-20/τ} ≈ 0,00798
Größte negative Abweichung am Ende der Blockade (t = 20 s):
y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % absolut)
Ende der Überdosierung (t = 40 s):
y(40) ≈ +6,3·10^{-7} (praktisch nominal)
Für t > 40 s klingt die winzige Restabweichung exponentiell ab:
y(t) = y(40) · e^{-(t-40)/τ}
Mit τ = 2495 s und x_B,in,0 = 0,00990099 ergeben sich:
e^{-20/τ} = e^{-20/2495} ≈ 0,99202; 1 - e^{-20/τ} ≈ 0,00798
Größte negative Abweichung am Ende der Blockade (t = 20 s):
y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % absolut)
Ende der Überdosierung (t = 40 s):
y(40) ≈ +6,3·10^{-7} (praktisch nominal)
Für t > 40 s klingt die winzige Restabweichung exponentiell ab:
y(t) = y(40) · e^{-(t-40)/τ}
Einordnung zur Mischgüte (CV = 3 %)
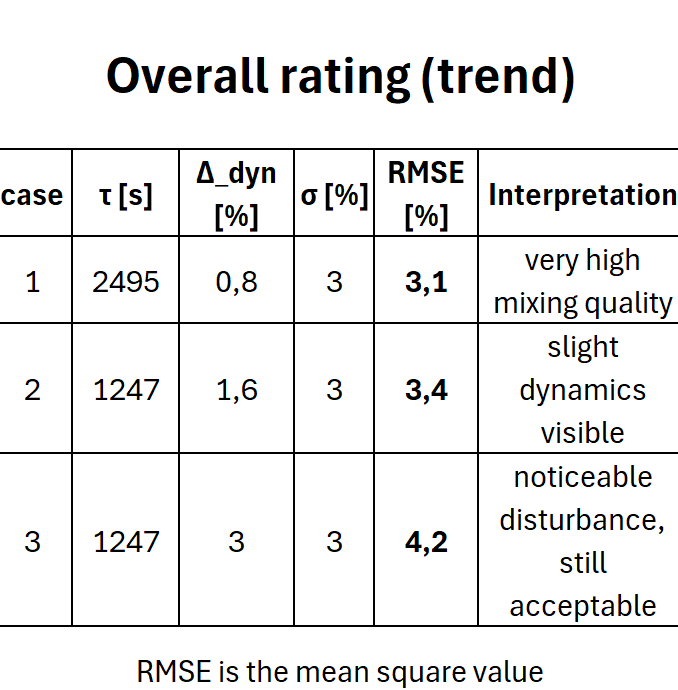
Die dynamische, durch die Störung verursachte Abweichung der B-Fraktion (~0,8 % relativ) liegt deutlich unter dem genannten Variationskoeffizienten der Mischgüte (3 %). Die Störung ist im Produktstrom daher praktisch kaum sichtbar.
Die dynamische, durch die Störung verursachte Abweichung der B-Fraktion (~0,8 % relativ) liegt deutlich unter dem genannten Variationskoeffizienten der Mischgüte (3 %). Die Störung ist im Produktstrom daher praktisch kaum sichtbar.
Nutzen der Laplace-Analyse
Die Laplace-Darstellung liefert eine geschlossene Formel für die zeitliche Auswirkung von Zulauf-Profilen auf die Auslass-Mischgüte. Damit lassen sich maximale Abweichungen, Erholzeiten und der Einfluss der Verweilzeit schnell abschätzen – hilfreich für die Auslegung von Mischraum und Korrekturstrategien.
Die Laplace-Darstellung liefert eine geschlossene Formel für die zeitliche Auswirkung von Zulauf-Profilen auf die Auslass-Mischgüte. Damit lassen sich maximale Abweichungen, Erholzeiten und der Einfluss der Verweilzeit schnell abschätzen – hilfreich für die Auslegung von Mischraum und Korrekturstrategien.
Wie verändert sich die Mischgüte, wenn die Massenströme doppelt so groß sind?
Wie verändert sich das Mischgüteresultat, wenn die Massenströme verdoppelt werden und sich die mittlere Verweilzeit von 41,6 Minuten auf 20,8 Minuten verkürzt? Pulver A fließt statt mit 1.000 kg/h nun mit 2.000 kg/h. Pulver B fließt statt 10 kg/h nun mit 20 kg/h. Es handelt sich um den gleichen kontinuierlichen Mischer AMK 1000 mit einer Drehfrequenz von 20 rpm, einem Füllgrad von 700 kg und den gleichen Komponenten A und B. Die Störung ist die gleiche: Komponente A fließt kontinuierlich, Komponente B ist für 20 Sekunden blockiert, danach fließt Komponente B für 20 Sekunden in doppelter Menge. Anschließend fließen die Komponenten regelkonform.
Fazit
Die relative Störabweichung am Auslass beträgt nun ca. 1,6 % (zuvor 0,8 %). Da sich die Verweilzeit halbiert hat, reagiert das System doppelt so schnell und zeigt eine etwa doppelt so große Amplitudenabweichung. Die Nennfraktion bleibt unverändert, daher skaliert der Effekt direkt mit 1 - e^{-20/τ}.
Einordnung zur Mischgüte (CV = 3 %)
Auch die 1,6 % relative dynamische Abweichung liegt unter dem Variationskoeffizienten der Mischgüte (3 %). Die Störung bleibt im Produktstrom moderat, ist aber sichtbar stärker als im ersten Fall.
Wie verändert sich das Mischgüteresultat, wenn die Massenströme verdoppelt werden und sich die mittlere Verweilzeit von 41,6 Minuten auf 20,8 Minuten verkürzt? Pulver A fließt statt mit 1.000 kg/h nun mit 2.000 kg/h. Pulver B fließt statt 10 kg/h nun mit 20 kg/h. Es handelt sich um den gleichen kontinuierlichen Mischer AMK 1000 mit einer Drehfrequenz von 20 rpm, einem Füllgrad von 700 kg und den gleichen Komponenten A und B. Die Störung ist die gleiche: Komponente A fließt kontinuierlich, Komponente B ist für 20 Sekunden blockiert, danach fließt Komponente B für 20 Sekunden in doppelter Menge. Anschließend fließen die Komponenten regelkonform.
Fazit
Die relative Störabweichung am Auslass beträgt nun ca. 1,6 % (zuvor 0,8 %). Da sich die Verweilzeit halbiert hat, reagiert das System doppelt so schnell und zeigt eine etwa doppelt so große Amplitudenabweichung. Die Nennfraktion bleibt unverändert, daher skaliert der Effekt direkt mit 1 - e^{-20/τ}.
Einordnung zur Mischgüte (CV = 3 %)
Auch die 1,6 % relative dynamische Abweichung liegt unter dem Variationskoeffizienten der Mischgüte (3 %). Die Störung bleibt im Produktstrom moderat, ist aber sichtbar stärker als im ersten Fall.
Was geschieht, wenn die dynamische Abweichung 3 % beträgt?
Was geschieht, wenn die dynamische Abweichung 3 % beträgt (statt 1,6 %) und damit in der Größenordnung der „Grundstreuung“ (CV = 3 %) liegt?Wie ist die Veränderung der Mischgüte zu bewerten, wenn aufgrund einer größeren Störung die relative dynamische Abweichung statt 1,6 % nun 3 % betragen würde? Ähnlich wie im störungsfreien Betrieb?
- Die dynamische Abweichung liegt nun in der Größenordnung des stationären CV.
Die Gesamtabweichung steigt auf über 4 %.
Qualität bleibt meist noch innerhalb ±5 %, aber Ausreißerrisiko erhöht sich deutlich.
Der kontinuierliche Mischer wirkt wie ein Tiefpassfilter. Eine Halbierung der Verweilzeit führt etwa zu einer Verdopplung der dynamischen Störabweichung. Solange diese unterhalb des Variationskoeffizienten bleibt, bleibt der Prozess robust. Wird sie gleich groß oder größer, addiert sie sich quadratisch zur Streuung – die Mischgüte verschlechtert sich spürbar, bleibt aber vorerst kontrollierbar.
Was geschieht, wenn die dynamische Abweichung 3 % beträgt (statt 1,6 %) und damit in der Größenordnung der „Grundstreuung“ (CV = 3 %) liegt?Wie ist die Veränderung der Mischgüte zu bewerten, wenn aufgrund einer größeren Störung die relative dynamische Abweichung statt 1,6 % nun 3 % betragen würde? Ähnlich wie im störungsfreien Betrieb?
- Die dynamische Abweichung liegt nun in der Größenordnung des stationären CV.
Die Gesamtabweichung steigt auf über 4 %.
Qualität bleibt meist noch innerhalb ±5 %, aber Ausreißerrisiko erhöht sich deutlich.
Der kontinuierliche Mischer wirkt wie ein Tiefpassfilter. Eine Halbierung der Verweilzeit führt etwa zu einer Verdopplung der dynamischen Störabweichung. Solange diese unterhalb des Variationskoeffizienten bleibt, bleibt der Prozess robust. Wird sie gleich groß oder größer, addiert sie sich quadratisch zur Streuung – die Mischgüte verschlechtert sich spürbar, bleibt aber vorerst kontrollierbar.
© Copyright by amixon GmbH