Analisi dei disturbi della qualità della miscelazione con trasformazione di Laplace
Esempio di applicazione della trasformata di Laplace per un processo di miscelazione continuo nel miscelatore amixon® AMK 1000: la polvere A fluisce costantemente nel miscelatore con una velocità di 1.000 kg/h. La polvere B viene dosata contemporaneamente con una velocità di 10 kg/h. All'inizio la camera di miscelazione rimane chiusa. L'utensile di miscelazione è già in funzione e raggiunge una qualità di miscelazione ideale dopo 20 giri. Gira a 20 giri/min.
Non appena nel miscelatore sono presenti 700 kg di prodotto, si apre la valvola di scarico. Lo scarico viene regolato in modo tale che i 1.010 kg/h in entrata vengano nuovamente scaricati. Il processo procede in modo stabile.
Improvvisamente si verifica un guasto: l'alimentazione del componente B si interrompe completamente per 20 secondi. Successivamente il dosatore viene corretto e B scorre per 20 secondi con una quantità doppia (20 kg/h). Infine, l'afflusso si stabilizza nuovamente a 10 kg/h.
Prima del guasto, la qualità della miscelazione era tecnicamente ideale. Il coefficiente di variazione della qualità della miscelazione era pari al 3%.
Il processo in cifre (situazione iniziale)
Afflusso A: ṁ_A = 1000 kg/h; afflusso B (nominale): ṁ_B = 10 kg/h; afflusso totale: ṁ_ein = 1010 kg/h. Massa costante di polvere nel miscelatore: M = 700 kg.
Tempo di permanenza medio τ (costante di tempo):
t = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s
Percentuale nominale di B all'ingresso (e stazionaria all'uscita):
x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)
Scenario di disturbo (afflusso B)
0 ≤ t < 20 s: Blocco, ṁ_B = 0; 20 ≤ t < 40 s:
Correzione, ṁ_B = 20 kg/h; t ≥ 40 s: di nuovo 10 kg/h.
Consideriamo la deviazione della frazione B nell'afflusso rispetto alla frazione nominale:
u(t) = x_B,in(t) − x_B,in,0.
Definizione parziale (flusso totale approssimativamente costante 1010 kg/h):
u(t) = {-x_B,in,0 per 0≤t<20 s; +x_B,in,0 per 20≤t<40 s; 0 per t≥40 s}
Soluzione di Laplace
Trasformata di Laplace del PT1:
Y(s) = (1 / (τ s + 1)) · U(s)
τ (Tau): la costante di tempo del sistema (in questo caso: il tempo medio di permanenza nel miscelatore)
s: la variabile di Laplace, una misura di come i segnali cambiano nel tempo
"τ · s" è una combinazione adimensionale della costante di tempo e del tasso di variazione.
Ingresso u(t) come differenza tra due salti rettangolari; con spostamenti di Heaviside si ottiene:
U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s
Soluzione nel dominio del tempo (sovrapposizione di risposte a gradino, Heaviside H(·)):
y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]
Valori numerici e scostamento massimo
Con τ = 2495 s e x_B,in,0 = 0,00990099 si ottiene:
e^{-20/τ} = e^{-20/2495} ≈ 0,99202; 1 - e^{-20/τ} ≈ 0,00798
Deviazione negativa massima alla fine del blocco (t = 20 s):
y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % assoluto)
Fine del sovradosaggio (t = 40 s):
y(40) ≈ +6,3·10^{-7} (praticamente nominale)
Per t > 40 s, la minuscola deviazione residua diminuisce in modo esponenziale:
y(t) = y(40) · e⁻^(t-40)/τ
Classificazione della qualità della miscela (CV = 3 %)
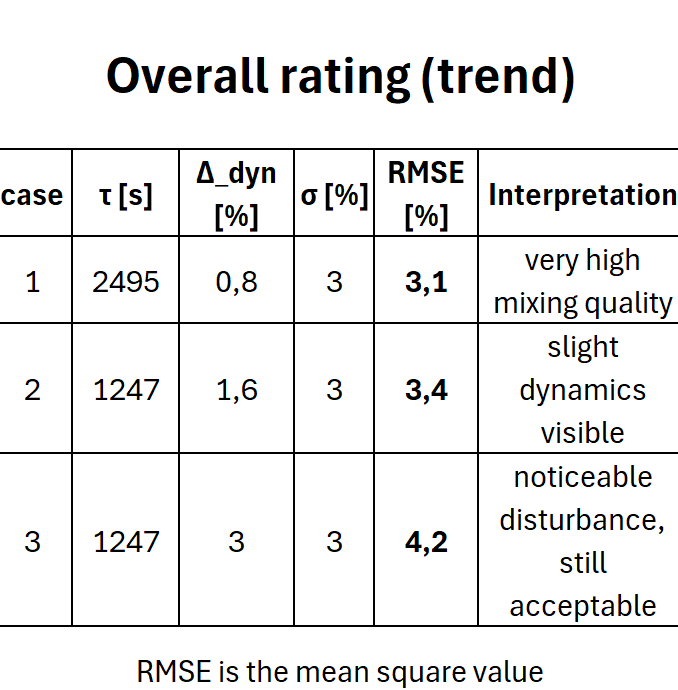
La deviazione dinamica della frazione B (~0,8 % relativo) causata dal disturbo è nettamente inferiore al coefficiente di variazione della qualità della miscelazione indicato (3 %). Il disturbo è quindi praticamente invisibile nel flusso del prodotto.
Vantaggi dell'analisi di Laplace
La rappresentazione di Laplace fornisce una formula chiusa per l'effetto temporale dei profili di afflusso sulla qualità di miscelazione in uscita. Ciò consente di valutare rapidamente le deviazioni massime, i tempi di recupero e l'influenza del tempo di permanenza, il che è utile per la progettazione della camera di miscelazione e delle strategie di correzione.
Come cambia la qualità della miscelazione quando i flussi di massa raddoppiano?
Come cambia il risultato della miscelazione quando i flussi di massa raddoppiano e il tempo di permanenza medio si riduce da 41,6 minuti a 20,8 minuti? La polvere A scorre ora a 2.000 kg/h invece che a 1.000 kg/h. La polvere B scorre ora a 20 kg/h invece che a 10 kg/h. Si tratta dello stesso miscelatore continuo AMK 1000 con una frequenza di rotazione di 20 giri/min, un grado di riempimento di 700 kg e gli stessi componenti A e B. Il guasto è lo stesso: il componente A scorre in modo continuo, il componente B è bloccato per 20 secondi, dopodiché il componente B scorre per 20 secondi in quantità doppia. Successivamente, i componenti scorrono in modo conforme alle regole.
Conclusione
La deviazione relativa del guasto all'uscita è ora di circa l'1,6% (in precedenza era dello 0,8%). Poiché il tempo di permanenza si è dimezzato, il sistema reagisce due volte più velocemente e mostra una deviazione di ampiezza circa doppia. La frazione nominale rimane invariata, quindi l'effetto è direttamente proporzionale a 1 - e^{-20/τ}.
Classificazione della qualità della miscelazione (CV = 3 %)
Anche la deviazione dinamica relativa dell'1,6 % è inferiore al coefficiente di variazione della qualità della miscelazione (3 %). Il disturbo rimane moderato nel flusso del prodotto, ma è visibilmente più forte rispetto al primo caso.
Cosa succede se la deviazione dinamica è pari al 3%?
Cosa succede se la deviazione dinamica è pari al 3% (anziché all'1,6%) e quindi dell'ordine di grandezza della “disperdizione di base” (CV = 3%)? Come valutare la variazione della qualità della miscelazione se, a causa di un guasto più grave, la deviazione dinamica relativa fosse pari al 3% anziché all'1,6%? In modo simile al funzionamento senza guasti?
- La deviazione dinamica è ora dell'ordine di grandezza del CV stazionario.
- La deviazione totale supera il 4%.
- La qualità rimane per lo più entro ±5%, ma il rischio di valori anomali aumenta in modo significativo.
Il miscelatore continuo agisce come un filtro passa-basso. Dimezzando il tempo di permanenza si ottiene circa un raddoppio della deviazione dinamica dovuta al disturbo. Finché questa rimane al di sotto del coefficiente di variazione, il processo rimane stabile. Se diventa uguale o superiore, si aggiunge in modo quadratico alla dispersione: la qualità della miscelazione peggiora sensibilmente, ma rimane per il momento controllabile.
© Copyright by amixon GmbH