Анализ нарушений качества смешивания с помощью преобразования Лапласа

Пример применения преобразования Лапласа для непрерывного процесса смешивания в смесителе amixon® AMK 1000: порошок A поступает в смеситель с постоянной скоростью 1000 кг/ч. Порошок B дозируется одновременно со скоростью 10 кг/ч. В начале смешивания смесительная камера остается закрытой. Смесительный механизм уже работает и после 20 оборотов достигает идеального качества смешивания. Он вращается со скоростью 20 об/мин.

Как только в смесителе накапливается 700 кг продукта, открывается сливной клапан. Слив регулируется таким образом, чтобы поступающие 1010 кг/ч снова выгружались. Процесс протекает стабильно.

Внезапно происходит сбой: подача компонента B полностью прекращается на 20 секунд. Затем дозатор корректируется, и B подается в течение 20 секунд с удвоенным количеством (20 кг/ч). Затем поток снова стабилизируется на уровне 10 кг/ч.

До возникновения неисправности качество смешивания было технически идеальным. Коэффициент вариации качества смешивания составлял 3 %.

Процесс в цифрах (исходная ситуация)

Подача A: ṁ_A = 1000 кг/ч; подача B (номинальная): ṁ_B = 10 кг/ч; общая подача: ṁ_ein = 1010 кг/ч. Постоянная масса порошка в смесителе: M = 700 кг.

Среднее время пребывания τ (постоянная времени):

t = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s

Номинальная массовая доля B на входе (и в стационарном режиме на выходе):

x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)

Сценарий сбоя (поток B)

0 ≤ t < 20 с: Блокада, ṁ_B = 0; 20 ≤ t < 40 с:

Корректировка, ṁ_B = 20 кг/ч; t ≥ 40 с: снова 10 кг/ч.

Мы рассматриваем отклонение доли B в поступлении относительно номинальной фракции:

u(t) = x_B,in(t) − x_B,in,0.

Детализированное определение (общий расход приблизительно постоянен 1010 кг/ч):

u(t) = {-x_B,in,0 для 0≤t<20 с; +x_B,in,0 для 20≤t<40 с; 0 для t≥40 с}

Динамическая модель (PT1, идеально перемешанная)

Доля на выходе y(t) (отклонение фракции B на выходе) соответствует модели PT1:

dy(t)/dt + y(t) = u(t), y(0⁻) = 0

Решение Лапласа

Преобразование Лапласа PT1:

Y(s) = (1 / (τ s + 1)) · U(s)

τ (тау): постоянная времени системы (здесь: среднее время пребывания в смесителе)
s: переменная Лапласа, мера изменения сигналов во времени
«τ · s» — безразмерная комбинация постоянной времени и скорости изменения.

Входной сигнал u(t) как разница двух прямоугольных скачков; с переносами Хевисайда получается:

U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s

Решение в временной области (суммирование ступенчатых откликов, Heaviside H(·)):

y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]

Числовые значения и максимальное отклонение

При τ = 2495 с и x_B,in,0 = 0,00990099 получаем:

e^{-20/τ} = e^{-20/2495} ≈ 0,99202; 1 - e^{-20/τ} ≈ 0,00798

Наибольшее отрицательное отклонение в конце блокировки (t = 20 с):

y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % в абсолютном выражении)

Конец передозировки (t = 40 с):

y(40) ≈ +6,3·10^{-7} (практически номинальное значение)

Для t > 40 с крошечное остаточное отклонение экспоненциально затухает:

y(t) = y(40) · e⁻^(t-40)/τ

Классификация по качеству смеси (CV = 3 %)

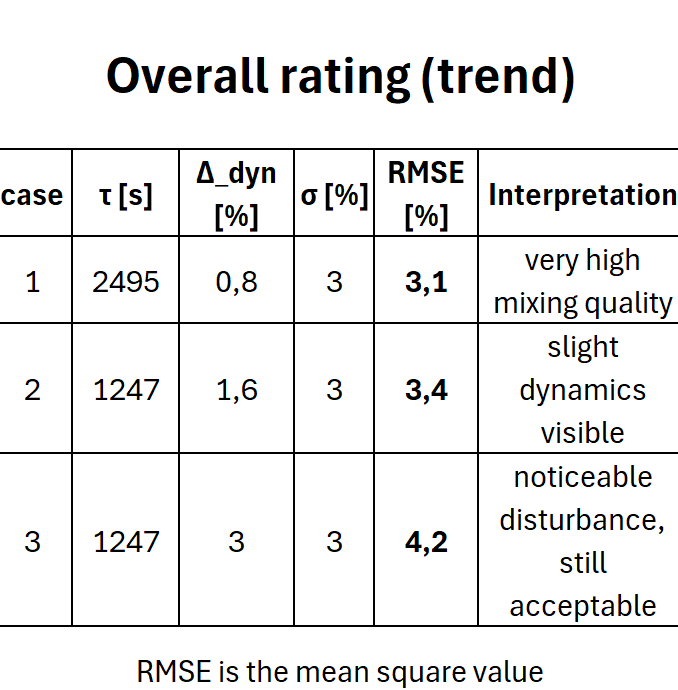
Динамическое отклонение фракции B (~0,8 % относительно), вызванное помехой, значительно ниже указанного коэффициента вариации качества смеси (3 %). Поэтому помеха практически незаметна в потоке продукта.

Преимущества анализа Лапласа

Представление Лапласа дает замкнутую формулу для временного воздействия профилей входящего потока на качество смешивания на выходе. Это позволяет быстро оценить максимальные отклонения, время восстановления и влияние времени пребывания, что полезно для проектирования смесительной камеры и стратегий корректировки.

Back