ラプラス変換による混合品質の障害分析

amixon®ミキサーAMK 1000における連続混合プロセスに対するラプラス変換の適用例：粉末Aは1,000 kg/hの一定流量でミキサーに流入します。粉末Bは同時に10 kg/hの流量で投入されます。混合室は開始時には閉じたままです。混合ツールはすでに作動しており、20 回転後に理想的な混合品質に達します。回転数は 20 rpm です。

ミキサーに 700 kg の製品が投入されると、排出バルブが開きます。流入する 1,010 kg/h が排出されるように排出量が調整されます。プロセスは安定して進行します。

突然、障害が発生します。成分 B の供給が 20 秒間完全に停止します。その後、投与装置が修正され、B が 20 秒間に 2 倍量（20 kg/h）で供給されます。その後、供給量は 10 kg/h に再び安定します。

障害発生前は、技術的に理想的な混合品質が得られていました。混合品質の変動係数は 3% でした。

プロセスを数字で見る（現状）

流入 A：ṁ_A = 1000 kg/h、流入 B（公称）：ṁ_B = 10 kg/h、総流入量：ṁ_ein = 1010 kg/h。ミキサー内の粉末質量定数：M = 700 kg。

平均滞留時間 τ（時間定数）：

t = M / ṁ_aus = 700 / 1010h = 0.693h = 41.6 分 = 2495 秒

流入部（および流出部で定常状態）における B の名目質量割合：

x_B,in,0 = 10 / 1010 = 0.00990099 (≈ 0.9901 %)

障害シナリオ（流入 B）

0 ≤ t < 20 s: 遮断状態、ṁ_B = 0;20 ≤ t < 40 s:

修正、ṁ_B = 20 kg/h; t ≥ 40 s: 再び 10 kg/h。

流入中のB成分の偏差を、公称分画に対して検討します。

u(t) = x_B,in(t) − x_B,in,0.

部分的な定義（総流量はおおよそ一定で 1010 kg/h）：

u(t) = {-x_B,in,0 (0≤t<20 sの場合); +x_B,in,0 (20≤t<40 sの場合); 0 (t≥40 sの場合)}

動的モデル（PT1、理想的な混合）

排出割合 y(t) (排出時の B フラクションの偏差) は PT1 モデルに従います。

dy(t)/dt + y(t) = u(t), y(0⁻) = 0

ラプラス解

PT1のラプラス変換：

Y(s) = (1 / (τ s + 1)) · U(s)

τ (タウ): システムの時間定数 (ここでは、ミキサー内の平均滞留時間)
s: ラプラス変数、信号が時間とともにどのように変化するかの尺度
「τ · s」は、時間定数と変化率の無次元組み合わせです。

入力 u(t) は 2 つの矩形ジャンプの差として、ヘビサイドシフトを用いて次のように表されます。

U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s

時間領域解（ステップ応答の重ね合わせ、Heaviside H(·)）：

y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]

数値と最大偏差

τ = 2495 s、x_B,in,0 = 0.00990099 を用いて、以下の結果が得られます。

e^{-20/τ} = e^{-20/2495} ≈ 0.99202; 1 - e^{-20/τ} ≈ 0.00798

ブロック終了時の最大負の偏差（t = 20 秒）：

y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % 絶対値)

過剰摂取の終了（t = 40 秒）：

y(40) ≈ +6.3×10^{-7} (実質的に公称値)

t > 40 s の場合、ごくわずかな残留偏差は指数関数的に減少します。

y(t) = y(40) · e⁻^(t-40)/τ

混合品質の分類（CV = 3%）

障害によって生じた B フラクションの動的な偏差（相対値で約 0.8%）は、混合品質の変動係数（3%）を大幅に下回っています。したがって、この障害は製品フローにはほとんど見られません。

ラプラス解析の利点

ラプラス表現は、流入プロファイルが流出混合品質に及ぼす時間的影響について、閉じた式を提供します。これにより、最大偏差、回復時間、滞留時間の影響を迅速に推定することができ、混合室の設計や修正戦略の立案に役立ちます。

質量流量が 2 倍になった場合、混合品質はどのように変化しますか？

質量流量が 2 倍になり、平均滞留時間が 41.6 分から 20.8 分に短縮された場合、混合品質はどのように変化しますか？粉末 A は 1,000 kg/h ではなく 2,000 kg/h で流れます。粉末 B は 10 kg/h ではなく 20 kg/h で流れます。これは、回転周波数 20 rpm、充填度 700 kg の同じ連続ミキサー AMK 1000 と、同じ成分 A および B を使用しています。障害は同じです。成分 A は連続的に流れ、成分 B は 20 秒間ブロックされた後、20 秒間に 2 倍の量で流れます。その後、コンポーネントは規則に従って流れます。

結論

出口での相対的な障害偏差は、約 1.6% (以前は 0.8%) になりました。滞留時間が半分になったため、システムの反応は 2 倍速くなり、振幅偏差も約 2 倍になりました。公称分率は変化しないため、この効果は 1 - e^{-20/τ} で直接スケーリングされます。

混合品質（CV = 3%）の分類

1.6% の相対的な動的偏差も、混合品質の変動係数（3%）を下回っています。製品フローにおける障害は中程度ですが、最初のケースよりも明らかに大きくなっています。

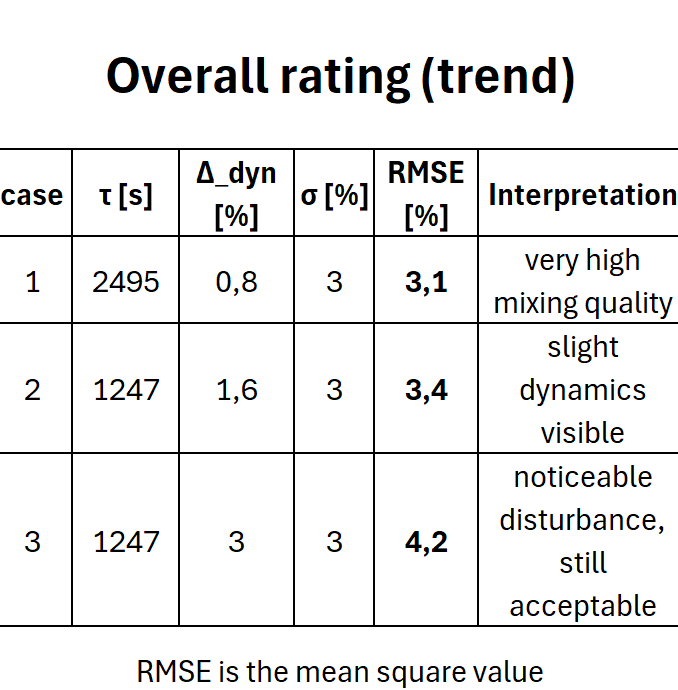
動的偏差が 3% の場合はどうなるか？

動的偏差が 3% (1.6% ではなく) となり、「基本分散」 (CV = 3%) の範囲内となった場合はどうなるのでしょうか？大きな障害により、相対的な動的偏差が 1.6% ではなく 3% となった場合、混合品質の変化はどのように評価されるのでしょうか？障害のない稼働時と同様でしょうか？

動的偏差は、定常 CV のオーダーになります。
総合偏差は 4% 以上になります。
品質は、ほとんどの場合 ±5% 以内に留まりますが、外れ値のリスクは大幅に高まります。

連続ミキサーはローパスフィルターのように機能します。滞留時間を半分にすると、動的障害偏差は約 2 倍になります。これが変動係数以下である限り、プロセスは堅調です。これが同等またはそれ以上になると、分散に 2 乗で加算されます。混合品質は著しく低下しますが、当面は制御可能なままです。