Analiza zaburzeń jakości mieszania za pomocą transformacji Laplace'a
Artykuł pokazuje, jak transformacja Laplace’a modeluje ciągły mieszalnik amixon AMK 1000 jako układ PT1 (stała czasowa = średni czas przebywania) i pozwala obliczyć wpływ krótkotrwałych zakłóceń dopływu składnika B. Przy nominalnych strumieniach zanik 20 s i potem 20 s nadmiaru daje na wylocie ok. 0,8% względnego odchylenia, wyraźnie poniżej CV = 3%. Po podwojeniu strumieni (i skróceniu czasu przebywania o połowę) odchylenie rośnie do ok. 1,6%, nadal <3%. Gdy odchylenie dynamiczne sięgnie 3%, łączne wahania przekroczą 4% (zwykle mieszczą się w ±5%), rośnie ryzyko wartości odstających; mieszalnik działa jak filtr dolnoprzepustowy, a skrócenie czasu przebywania zwiększa czułość na zakłócenia; analiza Laplace’a ułatwia szybkie szacunki amplitud, czasów regeneracji i dobór strategii.
Transformacja Laplace'a to matematyczna metoda obliczeniowa stosowana w systemach regulacyjnych w celu przejścia z „zakresu czasu” do „zakresu częstotliwości”.
Przykładowe zastosowanie transformacji Laplace'a dla ciągłego procesu mieszania w mieszalniku amixon® AMK 1000: Proszek A przepływa do mieszalnika ze stałą prędkością 1000 kg/h. Proszek B jest dozowany jednocześnie z prędkością 10 kg/h. Komora mieszania pozostaje na początku zamknięta. Narzędzie mieszające już pracuje i po 20 obrotach osiąga idealną jakość mieszania. Obraca się z prędkością 20 obr./min.
Gdy w mieszalniku znajdzie się 700 kg produktu, otwiera się zawór spustowy. Odpływ jest ustawiony tak, aby 1010 kg/h, które wpłynęło, zostało również wypuszczone. Proces przebiega stabilnie.
Nagle pojawia się zakłócenie: dopływ składnika B zostaje całkowicie zatrzymany na 20 sekund. Następnie dozownik zostaje skorygowany i składnik B przepływa przez 20 sekund z podwójną ilością (20 kg/h). Następnie dopływ ponownie stabilizuje się na poziomie 10 kg/h.
Przed wystąpieniem zakłócenia jakość mieszanki była idealna pod względem technicznym. Współczynnik zmienności jakości mieszanki wynosił 3%.
Proces w liczbach (sytuacja wyjściowa)
Dopływ A: ṁ_A = 1000 kg/h; dopływ B (nominalny): ṁ_B = 10 kg/h; całkowity dopływ: ṁ_ein = 1010 kg/h. Stała masa proszku w mieszalniku: M = 700 kg.
Średni czas przebywania τ (stała czasowa):
t = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s
Nominalna zawartość masowa B na wlocie (i stacjonarna na wylocie):
x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)
Dopływ A: ṁ_A = 1000 kg/h; dopływ B (nominalny): ṁ_B = 10 kg/h; całkowity dopływ: ṁ_ein = 1010 kg/h. Stała masa proszku w mieszalniku: M = 700 kg.
Średni czas przebywania τ (stała czasowa):
t = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s
Nominalna zawartość masowa B na wlocie (i stacjonarna na wylocie):
x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)
Scenariusz awarii (dopływ B)
0 ≤ t < 20 s: Blokada, ṁ_B = 0; 20 ≤ t < 40 s:
Korekta, ṁ_B = 20 kg/h; t ≥ 40 s: ponownie 10 kg/h.
Rozważamy odchylenie udziału frakcji B w dopływie względem frakcji nominalnej:
u(t) = x_B,in(t) − x_B,in,0.
Definicja częściowa (całkowity przepływ w przybliżeniu stały 1010 kg/h):
u(t) = {-x_B,in,0 dla 0≤t<20 s; +x_B,in,0 dla 20≤t<40 s; 0 dla t≥40 s}
0 ≤ t < 20 s: Blokada, ṁ_B = 0; 20 ≤ t < 40 s:
Korekta, ṁ_B = 20 kg/h; t ≥ 40 s: ponownie 10 kg/h.
Rozważamy odchylenie udziału frakcji B w dopływie względem frakcji nominalnej:
u(t) = x_B,in(t) − x_B,in,0.
Definicja częściowa (całkowity przepływ w przybliżeniu stały 1010 kg/h):
u(t) = {-x_B,in,0 dla 0≤t<20 s; +x_B,in,0 dla 20≤t<40 s; 0 dla t≥40 s}
Model dynamiczny (PT1, idealnie wymieszany)
Udział wylotu y(t) (odchylenie frakcji B na wylocie) jest zgodny z modelem PT1:
dy(t)/dt + y(t) = u(t), y(0⁻) = 0
Udział wylotu y(t) (odchylenie frakcji B na wylocie) jest zgodny z modelem PT1:
dy(t)/dt + y(t) = u(t), y(0⁻) = 0
Rozwiązanie Laplace'a
Przekształcenie Laplace'a PT1:
Y(s) = (1 / (τ s + 1)) · U(s)
τ (tau): stała czasowa systemu (w tym przypadku: średni czas przebywania w mieszalniku)
s: zmienna Laplace'a, miara zmian sygnałów w czasie
„τ · s” jest bezwymiarową kombinacją stałej czasowej i szybkości zmian.
Wejście u(t) jako różnica dwóch skoków prostokątnych; przy przesunięciach Heaviside'a otrzymujemy:
U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s
Rozwiązanie w dziedzinie czasu (nakładanie się odpowiedzi skokowych, Heaviside H(·)):
y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]
Przekształcenie Laplace'a PT1:
Y(s) = (1 / (τ s + 1)) · U(s)
τ (tau): stała czasowa systemu (w tym przypadku: średni czas przebywania w mieszalniku)
s: zmienna Laplace'a, miara zmian sygnałów w czasie
„τ · s” jest bezwymiarową kombinacją stałej czasowej i szybkości zmian.
Wejście u(t) jako różnica dwóch skoków prostokątnych; przy przesunięciach Heaviside'a otrzymujemy:
U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s
Rozwiązanie w dziedzinie czasu (nakładanie się odpowiedzi skokowych, Heaviside H(·)):
y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]
Wartości liczbowe i maksymalne odchylenie
Przy τ = 2495 s i x_B,in,0 = 0,00990099 otrzymujemy:
e^{-20/τ} = e^{-20/2495} ≈ 0,99202; 1 - e^{-20/τ} ≈ 0,00798
Największe ujemne odchylenie na końcu blokady (t = 20 s):
y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % bezwzględnie)
Koniec przedawkowania (t = 40 s):
y(40) ≈ +6,3·10^{-7} (praktycznie nominalna)
Dla t > 40 s niewielkie odchylenie resztkowe zanika wykładniczo:
y(t) = y(40) · e⁻^(t-40)/τ
Przy τ = 2495 s i x_B,in,0 = 0,00990099 otrzymujemy:
e^{-20/τ} = e^{-20/2495} ≈ 0,99202; 1 - e^{-20/τ} ≈ 0,00798
Największe ujemne odchylenie na końcu blokady (t = 20 s):
y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % bezwzględnie)
Koniec przedawkowania (t = 40 s):
y(40) ≈ +6,3·10^{-7} (praktycznie nominalna)
Dla t > 40 s niewielkie odchylenie resztkowe zanika wykładniczo:
y(t) = y(40) · e⁻^(t-40)/τ
Klasyfikacja jakości mieszanki (CV = 3%)
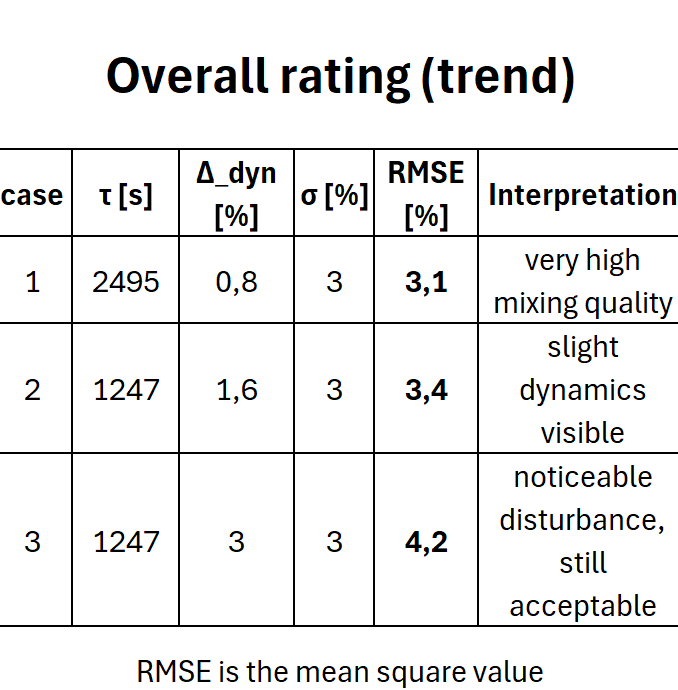
Dynamiczne odchylenie frakcji B (~0,8% względnie) spowodowane zakłóceniem jest znacznie niższe od podanego współczynnika zmienności jakości mieszanki (3%). Zakłócenie jest zatem praktycznie niewidoczne w strumieniu produktu.
Dynamiczne odchylenie frakcji B (~0,8% względnie) spowodowane zakłóceniem jest znacznie niższe od podanego współczynnika zmienności jakości mieszanki (3%). Zakłócenie jest zatem praktycznie niewidoczne w strumieniu produktu.
Korzyści płynące z analizy Laplace'a
Przedstawienie Laplace'a dostarcza zamkniętej formuły dla wpływu profili dopływu na jakość mieszania na wylocie w czasie. Dzięki temu można szybko oszacować maksymalne odchylenia, czasy regeneracji i wpływ czasu przebywania – co jest pomocne przy projektowaniu komory mieszania i strategii korekcyjnych.
Przedstawienie Laplace'a dostarcza zamkniętej formuły dla wpływu profili dopływu na jakość mieszania na wylocie w czasie. Dzięki temu można szybko oszacować maksymalne odchylenia, czasy regeneracji i wpływ czasu przebywania – co jest pomocne przy projektowaniu komory mieszania i strategii korekcyjnych.
Jak zmienia się jakość mieszanki, gdy strumienie masowe są dwukrotnie większe?
Jak zmienia się wynik mieszania, gdy strumienie masowe są dwukrotnie większe, a średni czas przebywania skraca się z 41,6 minuty do 20,8 minuty? Proszek A przepływa teraz z prędkością 2000 kg/h zamiast 1000 kg/h. Proszek B przepływa teraz z prędkością 20 kg/h zamiast 10 kg/h. Jest to ten sam mieszalnik ciągły AMK 1000 o częstotliwości obrotów 20 obr./min, stopniu wypełnienia 700 kg i tych samych składnikach A i B. Zakłócenie jest takie samo: składnik A przepływa w sposób ciągły, składnik B jest zablokowany przez 20 sekund, a następnie przepływa przez 20 sekund w podwójnej ilości. Następnie składniki płyną zgodnie z zasadami.
Wniosek
Względne odchylenie zakłócenia na wylocie wynosi teraz około 1,6% (wcześniej 0,8%). Ponieważ czas przebywania zmniejszył się o połowę, system reaguje dwa razy szybciej i wykazuje około dwukrotnie większe odchylenie amplitudy. Frakcja nominalna pozostaje niezmieniona, dlatego efekt skaluje się bezpośrednio z 1 - e^{-20/τ}.
Klasyfikacja jakości mieszania (CV = 3 %)
Również względne odchylenie dynamiczne wynoszące 1,6 % jest niższe od współczynnika zmienności jakości mieszania (3 %). Zakłócenie pozostaje umiarkowane w strumieniu produktu, ale jest wyraźnie silniejsze niż w pierwszym przypadku.
Jak zmienia się wynik mieszania, gdy strumienie masowe są dwukrotnie większe, a średni czas przebywania skraca się z 41,6 minuty do 20,8 minuty? Proszek A przepływa teraz z prędkością 2000 kg/h zamiast 1000 kg/h. Proszek B przepływa teraz z prędkością 20 kg/h zamiast 10 kg/h. Jest to ten sam mieszalnik ciągły AMK 1000 o częstotliwości obrotów 20 obr./min, stopniu wypełnienia 700 kg i tych samych składnikach A i B. Zakłócenie jest takie samo: składnik A przepływa w sposób ciągły, składnik B jest zablokowany przez 20 sekund, a następnie przepływa przez 20 sekund w podwójnej ilości. Następnie składniki płyną zgodnie z zasadami.
Wniosek
Względne odchylenie zakłócenia na wylocie wynosi teraz około 1,6% (wcześniej 0,8%). Ponieważ czas przebywania zmniejszył się o połowę, system reaguje dwa razy szybciej i wykazuje około dwukrotnie większe odchylenie amplitudy. Frakcja nominalna pozostaje niezmieniona, dlatego efekt skaluje się bezpośrednio z 1 - e^{-20/τ}.
Klasyfikacja jakości mieszania (CV = 3 %)
Również względne odchylenie dynamiczne wynoszące 1,6 % jest niższe od współczynnika zmienności jakości mieszania (3 %). Zakłócenie pozostaje umiarkowane w strumieniu produktu, ale jest wyraźnie silniejsze niż w pierwszym przypadku.
Co się stanie, jeśli odchylenie dynamiczne wyniesie 3%?
Co się stanie, jeśli odchylenie dynamiczne wyniesie 3% (zamiast 1,6%) i będzie zatem porównywalne z „rozproszeniem podstawowym” (CV = 3%)? Jak należy ocenić zmianę jakości mieszanki, jeśli z powodu większej awarii względne odchylenie dynamiczne wyniesie 3% zamiast 1,6%? Podobnie jak w przypadku pracy bez awarii?
- Odchylenie dynamiczne jest teraz rzędu stacjonarnego CV.
- Całkowite odchylenie wzrasta do ponad 4%.
- Jakość pozostaje zazwyczaj w granicach ±5%, ale ryzyko wystąpienia wartości odstających znacznie wzrasta.
Mieszalnik ciągły działa jak filtr dolnoprzepustowy. Skrócenie czasu przebywania o połowę powoduje podwojenie dynamicznego odchylenia zakłócenia. Dopóki pozostaje ono poniżej współczynnika zmienności, proces pozostaje stabilny. Jeśli osiągnie taką samą lub większą wartość, sumuje się kwadratowo do rozrzutu – jakość mieszania ulega zauważalnemu pogorszeniu, ale na razie pozostaje pod kontrolą.
Co się stanie, jeśli odchylenie dynamiczne wyniesie 3% (zamiast 1,6%) i będzie zatem porównywalne z „rozproszeniem podstawowym” (CV = 3%)? Jak należy ocenić zmianę jakości mieszanki, jeśli z powodu większej awarii względne odchylenie dynamiczne wyniesie 3% zamiast 1,6%? Podobnie jak w przypadku pracy bez awarii?
- Odchylenie dynamiczne jest teraz rzędu stacjonarnego CV.
- Całkowite odchylenie wzrasta do ponad 4%.
- Jakość pozostaje zazwyczaj w granicach ±5%, ale ryzyko wystąpienia wartości odstających znacznie wzrasta.
Mieszalnik ciągły działa jak filtr dolnoprzepustowy. Skrócenie czasu przebywania o połowę powoduje podwojenie dynamicznego odchylenia zakłócenia. Dopóki pozostaje ono poniżej współczynnika zmienności, proces pozostaje stabilny. Jeśli osiągnie taką samą lub większą wartość, sumuje się kwadratowo do rozrzutu – jakość mieszania ulega zauważalnemu pogorszeniu, ale na razie pozostaje pod kontrolą.
© Copyright by amixon GmbH