Analyse des perturbations de la qualité du mélange à l'aide de la transformation de Laplace
Exemple d'application de la transformation de Laplace pour un processus de mélange continu dans le mélangeur amixon® AMK 1000 : la poudre A s'écoule en continu à raison de 1 000 kg/h dans le mélangeur. La poudre B est dosée simultanément à raison de 10 kg/h. La chambre de mélange reste fermée au début. L'outil de mélange est déjà en marche et atteint une qualité de mélange idéale après 20 tours. Il tourne à 20 tr/min.
Dès que le mélangeur contient 700 kg de produit, la vanne de décharge s'ouvre. Le débit est réglé de manière à ce que les 1 010 kg/h entrants soient également déchargés. Le processus se déroule de manière stable.
Une perturbation survient soudainement : l'alimentation en composant B s'arrête complètement pendant 20 secondes. Le doseur est ensuite corrigé et B s'écoule pendant 20 secondes avec une quantité double (20 kg/h). L'alimentation se stabilise ensuite à nouveau à 10 kg/h.
Avant le dysfonctionnement, la qualité du mélange était techniquement parfaite. Le coefficient de variation de la qualité du mélange était de 3 %.
Le processus en chiffres (situation initiale)
Débit A : ṁ_A = 1000 kg/h ; débit B (nominal) : ṁ_B = 10 kg/h ; débit total : ṁ_ein = 1010 kg/h. Masse constante de poudre dans le mélangeur : M = 700 kg.
Temps de séjour moyen τ (constante de temps) :
t = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s
Part nominale de B à l'entrée (et stationnaire à la sortie) :
x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)
Débit A : ṁ_A = 1000 kg/h ; débit B (nominal) : ṁ_B = 10 kg/h ; débit total : ṁ_ein = 1010 kg/h. Masse constante de poudre dans le mélangeur : M = 700 kg.
Temps de séjour moyen τ (constante de temps) :
t = M / ṁ_aus = 700 / 1010 h = 0,693 h = 41,6 min = 2495 s
Part nominale de B à l'entrée (et stationnaire à la sortie) :
x_B,in,0 = 10 / 1010 = 0,00990099 (≈ 0,9901 %)
Scénario de perturbation (afflux B)
0 ≤ t < 20 s : Blocage, ṁ_B = 0 ; 20 ≤ t < 40 s :
Correction, ṁ_B = 20 kg/h ; t ≥ 40 s : à nouveau 10 kg/h.
Nous considérons l'écart de la fraction B dans l'alimentation par rapport à la fraction nominale :
u(t) = x_B,in(t) − x_B,in,0.
Définition partielle (débit total approximativement constant de 1010 kg/h) :
u(t) = {-x_B,in,0 pour 0≤t<20 s ; +x_B,in,0 pour 20≤t<40 s ; 0 pour t≥40 s}
0 ≤ t < 20 s : Blocage, ṁ_B = 0 ; 20 ≤ t < 40 s :
Correction, ṁ_B = 20 kg/h ; t ≥ 40 s : à nouveau 10 kg/h.
Nous considérons l'écart de la fraction B dans l'alimentation par rapport à la fraction nominale :
u(t) = x_B,in(t) − x_B,in,0.
Définition partielle (débit total approximativement constant de 1010 kg/h) :
u(t) = {-x_B,in,0 pour 0≤t<20 s ; +x_B,in,0 pour 20≤t<40 s ; 0 pour t≥40 s}
Modèle dynamique (PT1, mélange idéal)
Solution de Laplace
Transformée de Laplace du PT1 :
Y(s) = (1 / (τ s + 1)) · U(s)
τ (Tau) : la constante de temps du système (ici : le temps de séjour moyen dans le mélangeur)
s : la variable de Laplace, une mesure de la façon dont les signaux changent dans le temps
« τ · s » est une combinaison sans dimension de la constante de temps et du taux de changement.
Entrée u(t) comme différence entre deux sauts rectangulaires ; avec des décalages Heaviside, on obtient :
U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s
Solution dans le domaine temporel (superposition de réponses transitoires, Heaviside H(·)) :
y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]
Transformée de Laplace du PT1 :
Y(s) = (1 / (τ s + 1)) · U(s)
τ (Tau) : la constante de temps du système (ici : le temps de séjour moyen dans le mélangeur)
s : la variable de Laplace, une mesure de la façon dont les signaux changent dans le temps
« τ · s » est une combinaison sans dimension de la constante de temps et du taux de changement.
Entrée u(t) comme différence entre deux sauts rectangulaires ; avec des décalages Heaviside, on obtient :
U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s
Solution dans le domaine temporel (superposition de réponses transitoires, Heaviside H(·)) :
y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]
Valeurs numériques et écart maximal
Avec τ = 2495 s et x_B,in,0 = 0,00990099, on obtient :
e^{-20/τ} = e^{-20/2495} ≈ 0,99202 ; 1 - e^{-20/τ} ≈ 0,00798
Écart négatif maximal à la fin du blocage (t = 20 s) :
y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % absolu)
Fin du surdosage (t = 40 s) :
y(40) ≈ +6,3·10^{-7} (pratiquement nominal)
Pour t > 40 s, la minuscule déviation résiduelle diminue de manière exponentielle :
y(t) = y(40) · e⁻^(t-40)/τ
Avec τ = 2495 s et x_B,in,0 = 0,00990099, on obtient :
e^{-20/τ} = e^{-20/2495} ≈ 0,99202 ; 1 - e^{-20/τ} ≈ 0,00798
Écart négatif maximal à la fin du blocage (t = 20 s) :
y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7,9·10^{-5} (≈ -0,0079 % absolu)
Fin du surdosage (t = 40 s) :
y(40) ≈ +6,3·10^{-7} (pratiquement nominal)
Pour t > 40 s, la minuscule déviation résiduelle diminue de manière exponentielle :
y(t) = y(40) · e⁻^(t-40)/τ
Classification selon la qualité du mélange (CV = 3 %)
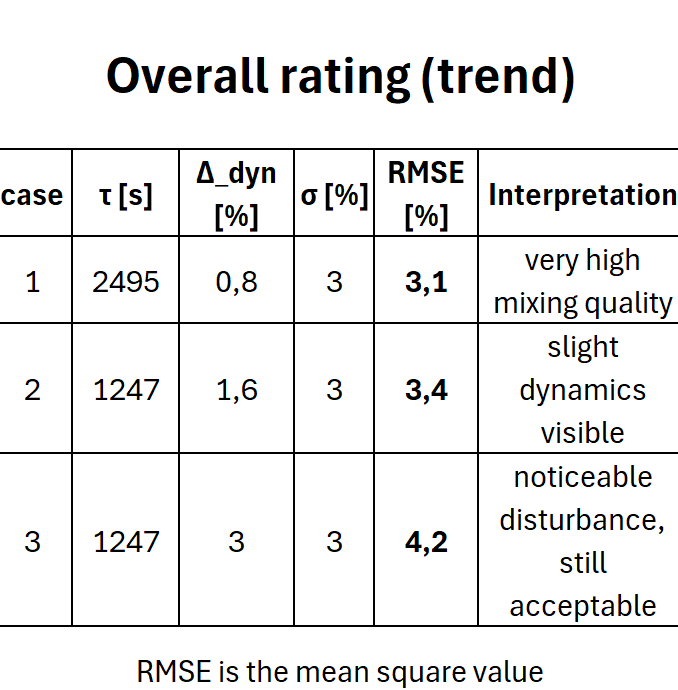
La variation dynamique de la fraction B (~0,8 % relatif) causée par le défaut est nettement inférieure au coefficient de variation indiqué pour la qualité du mélange (3 %). Le défaut est donc pratiquement invisible dans le flux de produit.
La variation dynamique de la fraction B (~0,8 % relatif) causée par le défaut est nettement inférieure au coefficient de variation indiqué pour la qualité du mélange (3 %). Le défaut est donc pratiquement invisible dans le flux de produit.
Avantages de l'analyse de Laplace
La représentation de Laplace fournit une formule fermée pour l'effet temporel des profils d'alimentation sur la qualité du mélange à la sortie. Cela permet d'estimer rapidement les écarts maximaux, les temps de récupération et l'influence du temps de séjour, ce qui est utile pour la conception de la chambre de mélange et les stratégies de correction.
La représentation de Laplace fournit une formule fermée pour l'effet temporel des profils d'alimentation sur la qualité du mélange à la sortie. Cela permet d'estimer rapidement les écarts maximaux, les temps de récupération et l'influence du temps de séjour, ce qui est utile pour la conception de la chambre de mélange et les stratégies de correction.
Comment la qualité du mélange évolue-t-elle lorsque les flux massiques sont deux fois plus importants ?
Comment le résultat du mélange change-t-il lorsque les flux massiques sont doublés et que le temps de séjour moyen passe de 41,6 minutes à 20,8 minutes ? La poudre A s'écoule désormais à 2 000 kg/h au lieu de 1 000 kg/h. La poudre B s'écoule désormais à 20 kg/h au lieu de 10 kg/h. Il s'agit du même mélangeur continu AMK 1000 avec une fréquence de rotation de 20 tr/min, un taux de remplissage de 700 kg et les mêmes composants A et B. Le dysfonctionnement est le même : le composant A s'écoule en continu, le composant B est bloqué pendant 20 secondes, puis le composant B s'écoule pendant 20 secondes en double quantité. Les composants s'écoulent ensuite conformément aux règles.
Conclusion
L'écart relatif de perturbation à la sortie est désormais d'environ 1,6 % (contre 0,8 % auparavant). Le temps de séjour ayant été divisé par deux, le système réagit deux fois plus vite et présente un écart d'amplitude environ deux fois plus important. La fraction nominale reste inchangée, l'effet est donc directement proportionnel à 1 - e^{-20/τ}.
Classification de la qualité du mélange (CV = 3 %)
L'écart dynamique relatif de 1,6 % est également inférieur au coefficient de variation de la qualité du mélange (3 %). La perturbation reste modérée dans le flux de produit, mais elle est visiblement plus forte que dans le premier cas.
Comment le résultat du mélange change-t-il lorsque les flux massiques sont doublés et que le temps de séjour moyen passe de 41,6 minutes à 20,8 minutes ? La poudre A s'écoule désormais à 2 000 kg/h au lieu de 1 000 kg/h. La poudre B s'écoule désormais à 20 kg/h au lieu de 10 kg/h. Il s'agit du même mélangeur continu AMK 1000 avec une fréquence de rotation de 20 tr/min, un taux de remplissage de 700 kg et les mêmes composants A et B. Le dysfonctionnement est le même : le composant A s'écoule en continu, le composant B est bloqué pendant 20 secondes, puis le composant B s'écoule pendant 20 secondes en double quantité. Les composants s'écoulent ensuite conformément aux règles.
Conclusion
L'écart relatif de perturbation à la sortie est désormais d'environ 1,6 % (contre 0,8 % auparavant). Le temps de séjour ayant été divisé par deux, le système réagit deux fois plus vite et présente un écart d'amplitude environ deux fois plus important. La fraction nominale reste inchangée, l'effet est donc directement proportionnel à 1 - e^{-20/τ}.
Classification de la qualité du mélange (CV = 3 %)
L'écart dynamique relatif de 1,6 % est également inférieur au coefficient de variation de la qualité du mélange (3 %). La perturbation reste modérée dans le flux de produit, mais elle est visiblement plus forte que dans le premier cas.
Que se passe-t-il lorsque l'écart dynamique est de 3 % ?
Que se passe-t-il lorsque l'écart dynamique est de 3 % (au lieu de 1,6 %) et se situe donc dans l'ordre de grandeur de la « dispersion de base » (CV = 3 %) ? Comment évaluer la modification de la qualité du mélange lorsque, en raison d'une perturbation importante, l'écart dynamique relatif passe de 1,6 % à 3 % ? De la même manière que dans le cas d'un fonctionnement sans perturbation ?
- L'écart dynamique est désormais de l'ordre de grandeur du CV stationnaire.
- L'écart total passe à plus de 4 %.
- La qualité reste généralement dans une fourchette de ±5 %, mais le risque d'écarts extrêmes augmente considérablement.
Le mélangeur continu agit comme un filtre passe-bas. Une réduction de moitié du temps de séjour entraîne environ un doublement de l'écart dynamique dû aux perturbations. Tant que celui-ci reste inférieur au coefficient de variation, le processus reste robuste. S'il devient égal ou supérieur, il s'ajoute de manière quadratique à la dispersion – la qualité du mélange se détériore sensiblement, mais reste contrôlable pour l'instant.
Que se passe-t-il lorsque l'écart dynamique est de 3 % (au lieu de 1,6 %) et se situe donc dans l'ordre de grandeur de la « dispersion de base » (CV = 3 %) ? Comment évaluer la modification de la qualité du mélange lorsque, en raison d'une perturbation importante, l'écart dynamique relatif passe de 1,6 % à 3 % ? De la même manière que dans le cas d'un fonctionnement sans perturbation ?
- L'écart dynamique est désormais de l'ordre de grandeur du CV stationnaire.
- L'écart total passe à plus de 4 %.
- La qualité reste généralement dans une fourchette de ±5 %, mais le risque d'écarts extrêmes augmente considérablement.
Le mélangeur continu agit comme un filtre passe-bas. Une réduction de moitié du temps de séjour entraîne environ un doublement de l'écart dynamique dû aux perturbations. Tant que celui-ci reste inférieur au coefficient de variation, le processus reste robuste. S'il devient égal ou supérieur, il s'ajoute de manière quadratique à la dispersion – la qualité du mélange se détériore sensiblement, mais reste contrôlable pour l'instant.
© Copyright by amixon GmbH