Konzentrationsgradient

Wenn sich Stoffe ohne mechanische Förderung bewegen, wirkt der Konzentrationsgradient als treibende Kraft. Zum Beispiel für Diffusion oder Wärmeübergang.

In der Lebensmittel- und Pharmatechnik spielen sie ebenfalls eine bedeutende Rolle. Instantprodukte lösen sich rasch auf, da die Porenstrukturen den Transport begünstigen. Tabletten geben Wirkstoffe über Diffusion entlang eines Konzentrationsgradienten frei.

In der Stoffübertragung sind sie der Antrieb für Diffusion. Bei der Trocknung diffundiert beispielsweise Wasser aus dem Inneren von Partikeln nach außen. In der Gaswäsche wandern Gasmoleküle in ein Lösungsmittel. Auch bei der Extraktion, beispielsweise von Koffein aus Kaffeebohnen, erfolgt der Transport entlang eines Konzentrationsgefälles.

In der Trenntechnik sind Konzentrationsunterschiede der Antrieb für viele Prozesse. In Membrananlagen wie der Umkehrosmose oder der Dialyse fließt der Stoffstrom durch die Membran entlang eines Gefälles.

Auch in der Umwelttechnik spielen Konzentrationsgradienten eine treibende Rolle. Schadstoffe bewegen sich durch Böden und Porenräume entlang ihrer Konzentrationsgefälle. In Brennstoffzellen bestimmen Gradienten den Transport von Reaktanten und Produkten.

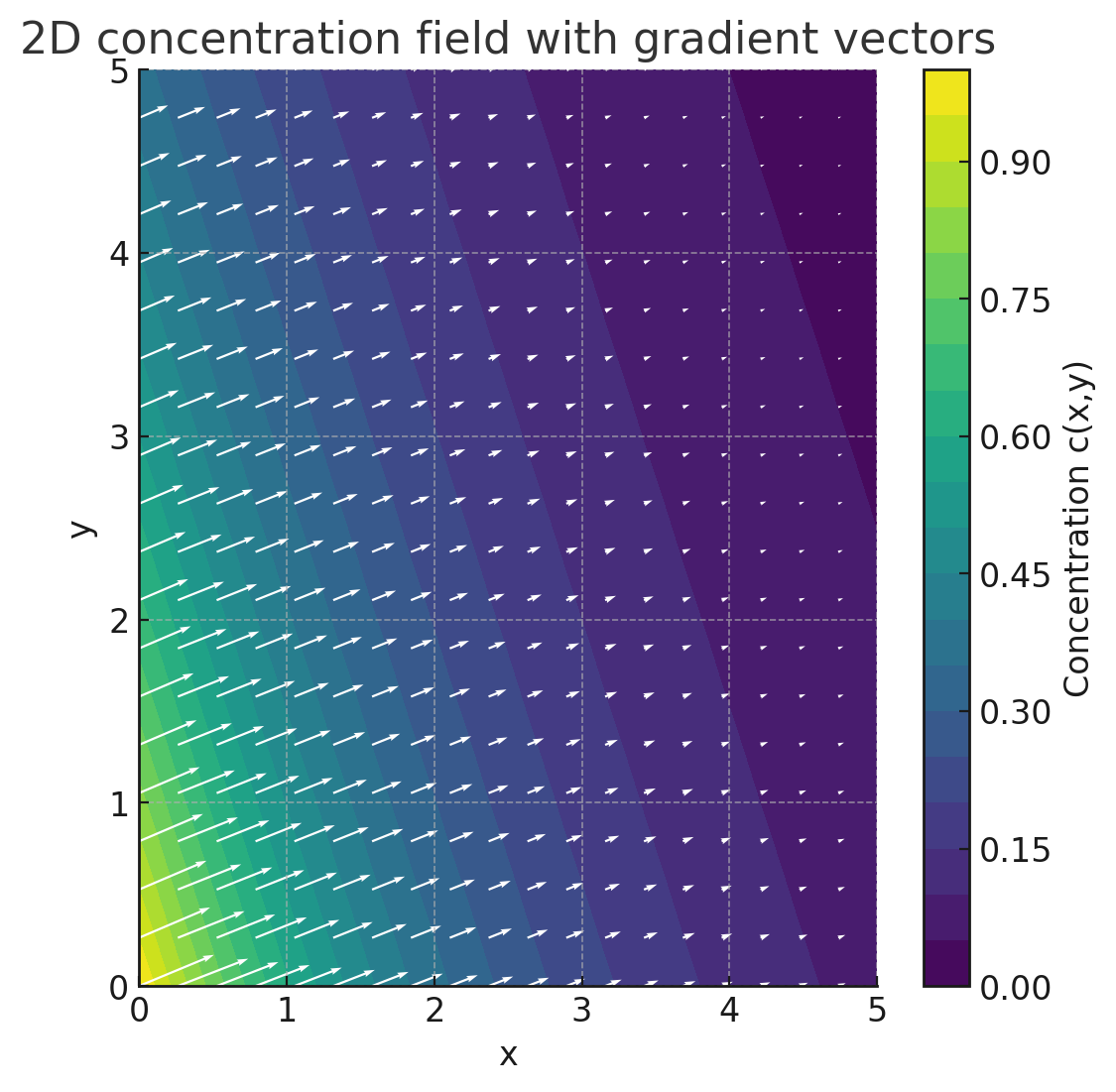
Ein Konzentrationsgradient beschreibt die räumliche Änderung der Konzentration einer Substanz. Er gibt an, wie stark sich die Konzentration c pro Längeneinheit x verändert.

Mathematisch wird er als Vektor definiert, der nach dem Weg differenziert wird.

dc/dx = ∇c = (∂x/∂c, ∂y/∂c, ∂z/∂c)

Eine Möglichkeit der zweidimensionalen vektoriellen Darstellung ist links gezeigt. Die Länge der Vektoren zeigt das Konzentrationsgefälle. Die Pfeilrichtung der Vektoren zeigt am jeweiligen Ort die Richtung der angestrebten Diffusion an.