Gradient de concentration

Lorsque des substances se déplacent sans être transportées mécaniquement, le gradient de concentration agit comme une force motrice. Par exemple pour la diffusion ou le transfert de chaleur.

Ils jouent également un rôle important dans l'industrie alimentaire et pharmaceutique. Les produits instantanés se dissolvent rapidement, car les structures poreuses favorisent le transport. Les comprimés libèrent les substances actives par diffusion le long d'un gradient de concentration.

Dans le transfert de masse, ils sont le moteur de la diffusion. Lors du séchage, par exemple, l'eau se diffuse de l'intérieur des particules vers l'extérieur. Dans le lavage de gaz, les molécules de gaz migrent dans un solvant. Lors de l'extraction, par exemple de la caféine des grains de café, le transport se fait également le long d'un gradient de concentration.

Dans les techniques de séparation, les différences de concentration sont le moteur de nombreux processus. Dans les installations à membrane telles que l'osmose inverse ou la dialyse, le flux de substances s'écoule à travers la membrane le long d'une pente.

Les gradients de concentration jouent également un rôle moteur dans les techniques environnementales. Les polluants se déplacent à travers les sols et les espaces interstitiels le long de leurs gradients de concentration. Dans les piles à combustible, les gradients déterminent le transport des réactifs et des produits.

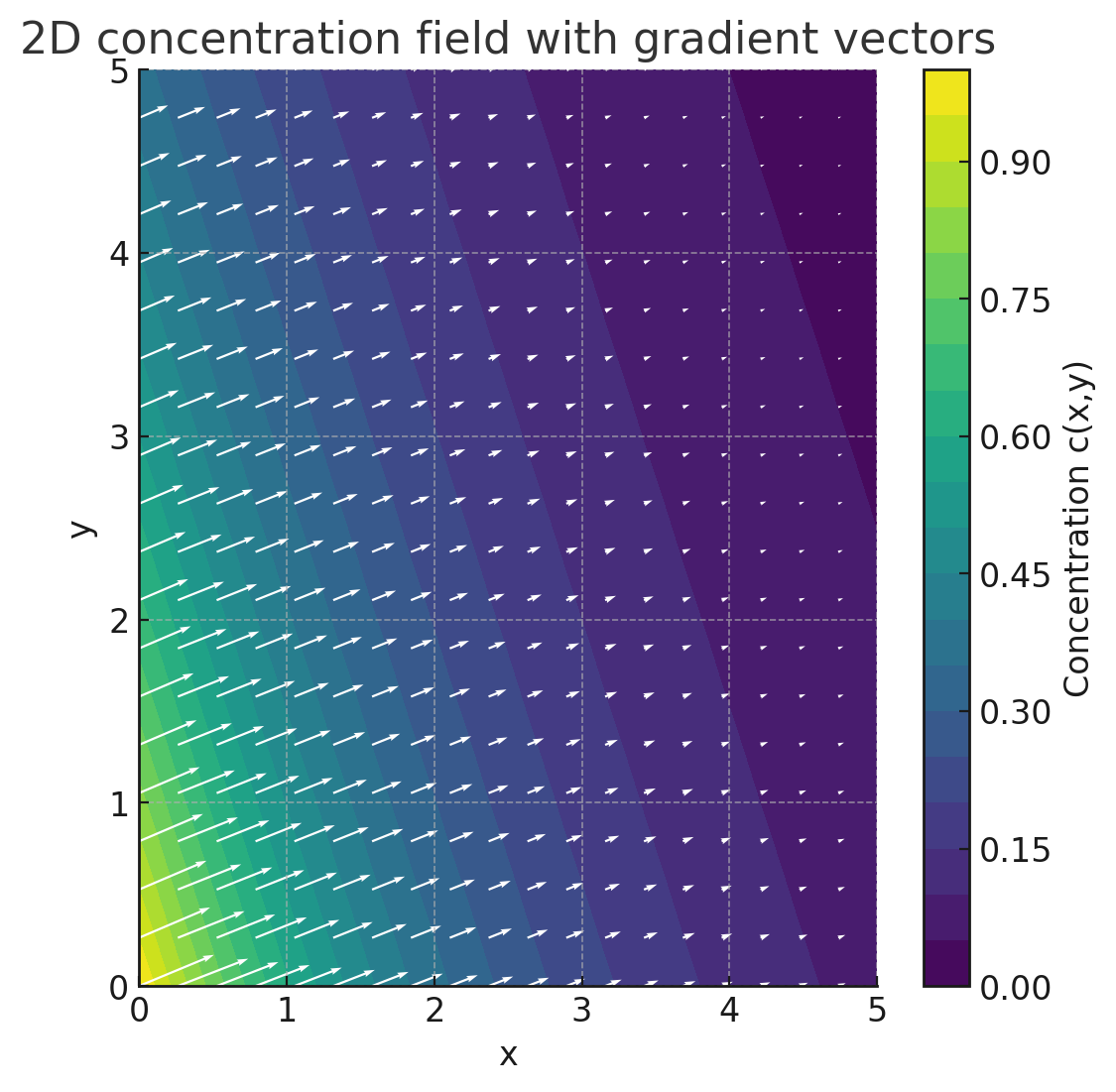
Un gradient de concentration décrit la variation spatiale de la concentration d'une substance. Il indique l'ampleur de la variation de la concentration c par unité de longueur x.

Mathématiquement, il est défini comme un vecteur qui est différencié en fonction du chemin.

dc/dx = ∇c = (∂x/∂c, ∂y/∂c, ∂z/∂c)

Une possibilité de représentation vectorielle bidimensionnelle est montrée à gauche. La longueur des vecteurs indique le gradient de concentration. La direction des flèches des vecteurs indique à chaque endroit la direction de la diffusion visée.