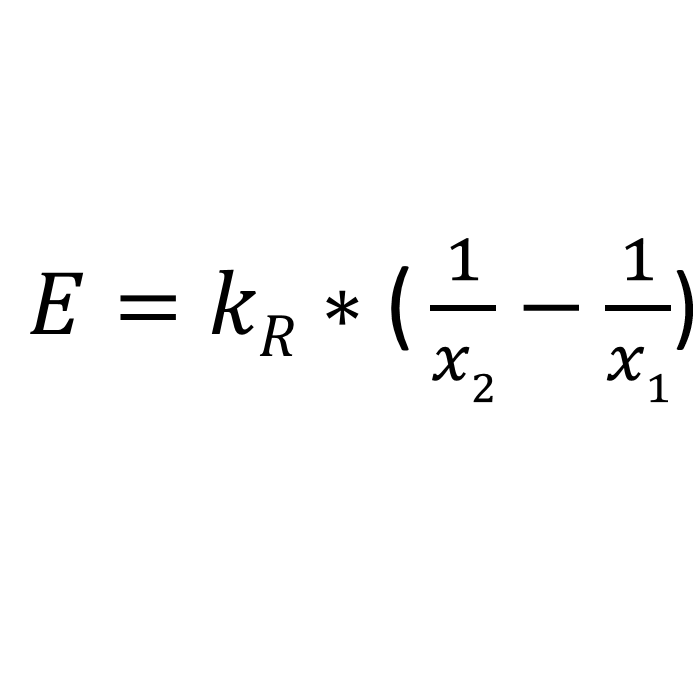
Analyse dimensionnelle

L'analyse dimensionnelle aide à développer des formules de calcul basées sur l'expérimentation.

L'analyse dimensionnelle est une méthode qui permet de ramener les grandeurs physiques à leurs unités de base (p. ex. longueur, temps, masse) et de les traduire en équations cohérentes avec les unités, généralement sur la base du Système international d'unités (SI). Dans le domaine de la technique des procédés expérimentaux, elle sert souvent à convertir des phénomènes observés empiriquement en formules qui restent valables indépendamment du système d'unités utilisé.

De telles équations permettent une description quantitative des effets de procédés, par exemple lors du concassage, du broyage, de l'agglomération ou de la dispersion. Même si elles semblent formellement correctes sur le plan physique, elles reposent essentiellement sur des relations observées. Les lois physiques sous-jacentes n'ont pas encore été découvertes. On parle donc d'approximations cohérentes du point de vue de l'analyse dimensionnelle.

Dans la pratique, l'analyse dimensionnelle est un outil précieux pour la modélisation, la mise à l'échelle et le transfert des résultats des essais en laboratoire technique vers les processus industriels.

La loi Rittinger en est un exemple. Cette équation repose sur l'hypothèse que l'énergie nécessaire au broyage est proportionnelle à la nouvelle surface générée, ce qui est relativement vrai pour le broyage fin.

• E : Besoin énergétique spécifique (par ex. kJ/kg)
• x1 : diamètre initial du grain (m)
• x2 : diamètre du grain final (m)
• kR : constante de Rittinger ; dépend du matériau dans la dimension : [m³/s²])