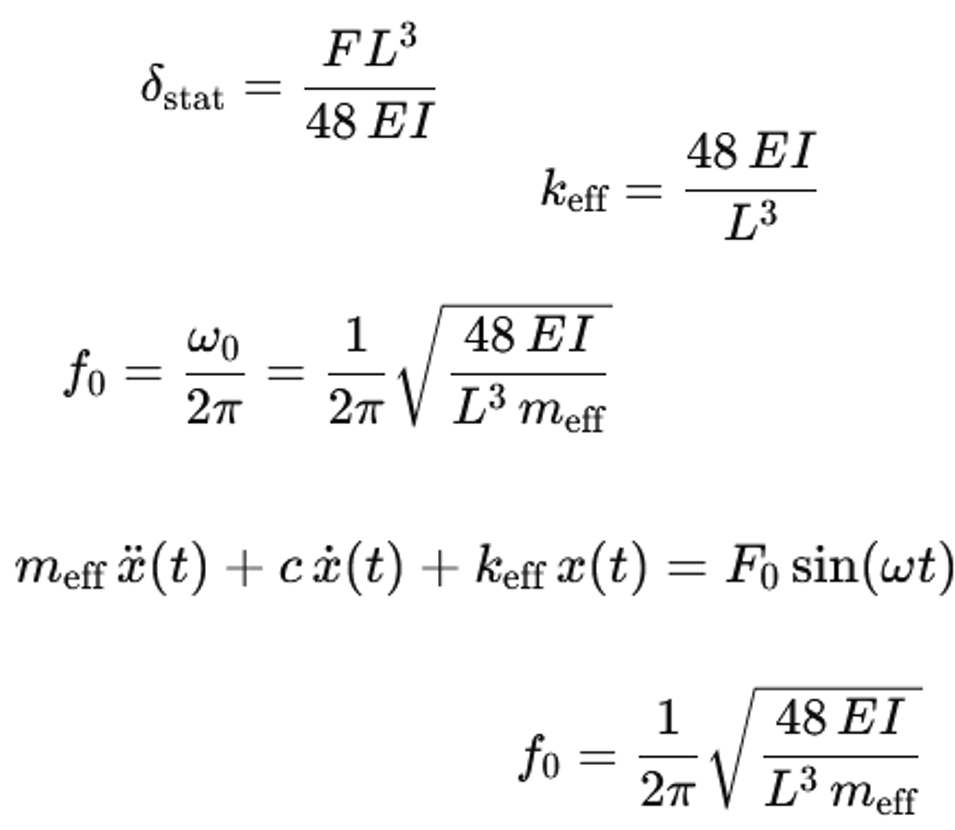resonance frequencies
This is an initial assessment of the probability of this being a vibration problem with a risk of resonance. The following derivation refers to an amixon® ring layer mixing granulator. The situation is highly idealised.
The ring layer mixing granulator is mounted centrally on a single-bearing support. It is considered a point load. This rests on two supports on the right and left like a bridge. The machine has a drive motor and a rotating mixing shaft. The motor and shaft rotate at a speed of n [revolutions per minute]. The mixing shaft has a small imbalance. This generates a periodic vertical force in the centre of the support. For estimation purposes, the system is modelled as a single-mass oscillator. The support is considered to be a spring with a spring stiffness keff. The machine and part of the support are considered to be an effective mass m_(eff). The imbalance generates a harmonic excitation force F(t). The following data is to be estimated:
- excitation frequency
- unbalance effects
- theoretical spring stiffness
- Natural frequency of the entire system
Excitation frequency of the imbalance
The rotational speed n is given in revolutions per minute. The excitation frequency in hertz is calculated from the rotational speed. The excitation frequency fExcitation in hertz is: f_Excitation = n / 60. The excitation angular frequency ω is:
ω = 2 * π * f_Erreger = 2 * π * n / 60
ω = 2 π n/60
Example: At n = 600 revolutions per minute, f_exciter = 10 hertz.
In the ring layer mixing granulator, the mixing chamber is hinged open.
Imbalance effects and imbalance force
The imbalance is described by an imbalance mass mu. The imbalance mass mu is located at a distance e from the axis of rotation. The imbalance experiences a centripetal force during rotation. The amplitude of the imbalance force F0 is:
F0 = mu e ω2
The time-dependent excitation force F(t) can be assumed to be sinusoidal. The excitation force is then written as:
F(t) = F0 sin (ω t)
This force acts vertically in the centre of the beam.
Theoretical spring stiffness of the beam in the middle of the field
The beam is considered to be a simply supported beam with a point load at its centre. The span of the beam is L. The bending stiffness of the beam is given by the product E * I. E is the modulus of elasticity of the steel. I is the area moment of inertia of the cross-section. A static vertical force F acts at the centre of the beam. The static deflection δ_stat at the centre of the beam is:
δstat = F L3/ (48 E I)
The spring stiffness k_eff is defined as force divided by displacement. When applied, this results in:
keff = F / δstat = 48 E I / L3
The spring stiffness k_eff describes the vertical stiffness of the beam in the middle of the span.
Ring layer mixing granulator.
Effective mass m_eff of the system
The oscillating mass consists of the mass of the machine and a proportion of the carrier mass. The mass of the machine is m_M. The mass of the carrier is m_B. Not all parts of the carrier vibrate equally strongly. Therefore, a participation factor η is used. The participation factor is often between 0.2 and 0.3. A commonly used simplification is η = 0.25. The effective mass m_eff is then calculated as the sum:
meff = mM + η mB
If the machine mass is significantly greater than the carrier mass, m_eff ≈ m_M can be set as an approximation.
Natural frequency of the entire system
The system is considered as a single-mass oscillator with mass m_eff and spring stiffness k_eff. The differential equation of the undamped single-mass oscillator is:
meff x¨(t) + keff x(t) = 0
The natural frequency ω₀ is:
ω0 = sqrt (keff/meff)
The natural frequency f_0 in hertz is:
f0 = ω0 / (2π)
f0 = (1 / (2 π)) sqrt (keff / meff)
If k_eff is replaced by 48 * E * I / L^3, the result is:
f0 = (1 / (2 π)) sqrt ((48 E I) / (L3 meff))
This formula shows that the natural frequency increases with the bending stiffness E * I and decreases with the span L and the effective mass m_eff.
Comparison of excitation frequency and natural frequency to estimate the risk of resonance
The excitation frequency f_excitation is calculated from the speed of the machine. The natural frequency f_0 is calculated from the spring stiffness of the support and the effective mass. There is a risk of resonance if the excitation frequency is close to the natural frequency. The resonance condition is approximately:
fErreger ≈ f0
For a safe design, there should be a gap between the natural frequency and the excitation frequency. A gap of around 20 per cent or more is often chosen as a guideline value. If the natural frequency is significantly above the entire speed range, the risk of resonance is low. If the natural frequency is significantly below the entire speed range, the risk of resonance is also low. If the natural frequency is within the speed range used, a vibration problem is likely.
This derivation allows an initial assessment of whether a resonance problem is to be expected with the ring layer mixed agglomerator on a carrier.
After completion, amixon® agglomerators undergo a balancing treatment. This eliminates both static and dynamic imbalances. In addition, the machines are mounted on damping systems. These decouple any vibrations that may occur from the foundation and prevent noise.
© Copyright by amixon GmbH