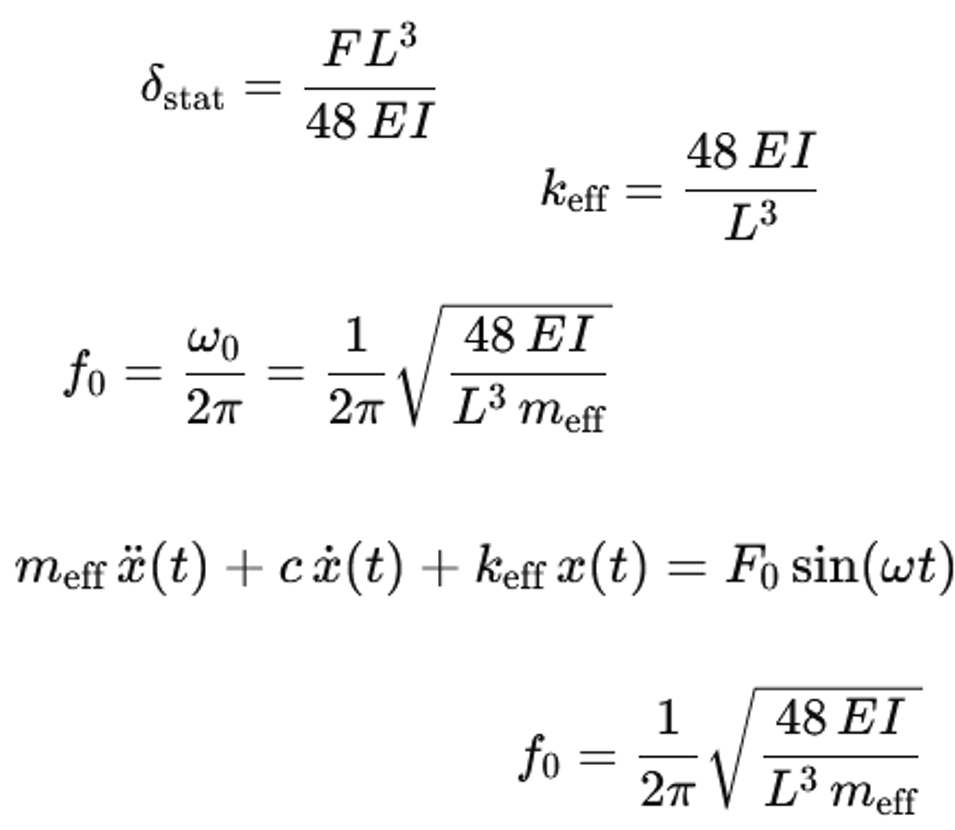共振周波数を測定する
これは、共振の危険を伴う振動の問題である可能性の初期評価に関するものです。以下の導出は、amixon® リング層混合造粒機に関するものです。この事実は非常に理想化されたものです。
リング層混合造粒機は、単軸支持のキャリアの中央に取り付けられています。これは点荷重と見なされます。これは、橋のように左右2つの支持部に載っています。この機械は、駆動モーターと回転式混合シャフトを備えています。モーターとシャフトは、回転数 n [回転/分] で回転します。混合シャフトにはわずかなアンバランスがあります。これにより、支持体の中央に周期的な垂直力が発生します。推定のために、このシステムは単質量振動子としてモデル化されます。支持体は、ばね定数 keff のばねとして扱われます。機械と支持体の一部は、有効質量 m_(eff) として扱われます。不均衡により、調和励起力 F(t) が発生します。以下のデータを推定します。
- 励起周波数
- 不均衡効果
- 理論上のばね定数
- システム全体の固有振動数
アンバランス振動の励起周波数
回転数 n は 1 分あたりの回転数で表されます。回転数から、励磁周波数をヘルツ単位で計算します。励磁周波数 fErreger（ヘルツ）は、f_Erreger = n / 60 です。励磁円周波数 ω は、
ω = 2 * π * f_Erreger = 2 * π * n / 60
ω = 2 π n/60
例：n = 600 回転/分の場合、f_励磁 = 10 ヘルツとなります。
リング層混合造粒機では、混合室は開いています。
フィールド中央における梁の理論上のばね定数
梁は、中央に点荷重がかかる単支点梁と見なされます。梁のスパンは L です。梁の曲げ剛性は、E * I の積によって与えられます。E は鋼の弾性係数です。I は断面積の二次モーメントです。静的な垂直力 F が梁の中央に作用します。梁の中央における静的なたわみ δ_stat は、次の式で求められます。
δstat = F L3/ (48 E I)
ばね定数 k_eff は、力を変位で割った値として定義されます。これを適用すると、次の式が得られます。
keff = F / δstat = 48 E I / L3
ばね剛性 k_eff は、梁の中央部の垂直方向の剛性を表します。
リング層混合造粒機。
システム全体の固有振動数
このシステムは、質量 m_eff およびばね定数 k_eff を有する単質量振動子と見なされます。減衰のない単質量振動子の微分方程式は次のとおりです。
meff x¨(t) + keff x(t) = 0
固有角周波数 ω_0 は次のとおりです。
ω0 = sqrt (keff/meff)
固有振動数 f_0（ヘルツ単位）は次のとおりです。
f0 = ω0 / (2π)
f0 = (1 / (2 π)) sqrt (keff / meff)
k_eff を 48 * E * I / L^3 で置き換えると、次の式が得られます。
f0 = (1 / (2 π)) sqrt ((48 E I) / (L3 meff))
この式は、固有振動数が曲げ剛性 E * I に比例し、スパン L および有効質量 m_eff に反比例することを示しています。
共振の危険性を評価するための励起周波数と固有周波数の比較
励起周波数 f_Erreger は、機械の回転数から計算されます。固有周波数 f_0 は、梁のばね定数と有効質量から計算されます。励起周波数が固有周波数に近い場合、共振の危険性があります。共振条件は、おおよそ以下のようになります。
fErreger ≈ f0
安全な設計のためには、固有振動数と励起周波数との間に間隔を設ける必要があります。多くの場合、約 20% 以上の差を基準値として選択します。固有振動数が全回転数範囲を大幅に上回っている場合、共振の危険性は低くなります。固有振動数が全回転数範囲を大幅に下回っている場合も、共振の危険性は低くなります。固有振動数が使用回転数範囲内にある場合、振動の問題が発生する可能性が高くなります。
この導出により、リング層混合アグリゲーターがキャリア上で共振の問題が発生するかどうかについて、最初の評価を行うことができます。
完成後、amixon® のアグリゲーターはバランス調整処理が施されます。これにより、静的および動的な不均衡が解消されます。さらに、機械は減衰システム上に設置されています。これにより、発生する可能性のある振動が基礎から分離され、騒音が防止されます。
© Copyright by amixon GmbH