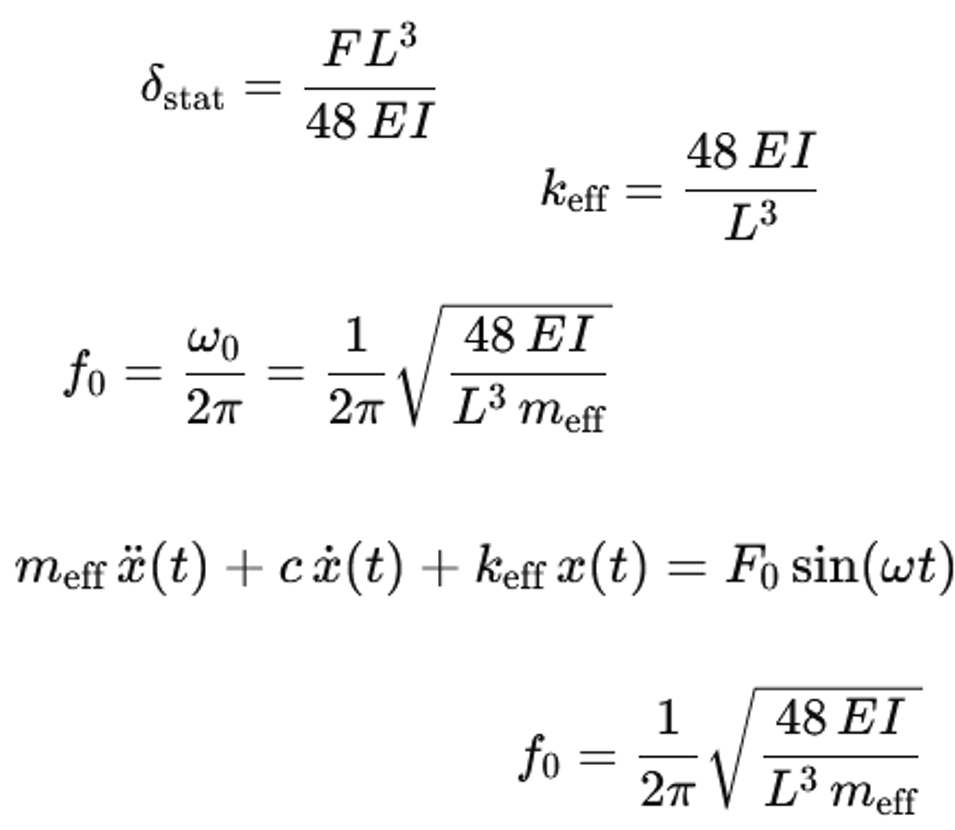Déterminer les fréquences de résonance
Il s'agit d'une première estimation de la probabilité qu'il s'agisse d'un problème de vibrations avec risque de résonance. Le raisonnement suivant se réfère à un granulateur mélangeur à couche annulaire amixon®. La situation est fortement idéalisée.
Le granulateur mélangeur à couche annulaire est monté au centre sur un support à palier simple. Il est considéré comme une charge ponctuelle. Il repose à droite et à gauche comme un pont sur deux appuis. La machine dispose d'un moteur d'entraînement et d'un arbre mélangeur rotatif. Le moteur et l'arbre tournent à une vitesse n [tours par minute]. L'arbre mélangeur présente un léger déséquilibre. Celui-ci génère une force verticale périodique au centre du support. Pour l'estimation, le système est modélisé comme un oscillateur à masse unique. Le support est considéré comme un ressort avec une rigidité keff. La machine et une partie du support sont considérées comme une masse effective m_(eff). Le déséquilibre génère une force d'excitation harmonique F(t). Les données suivantes doivent être estimées :
- fréquence d'excitation
- effets de déséquilibre
- rigidité théorique du ressort
- Fréquence propre de l'ensemble du système
Fréquence d'excitation du déséquilibre
La vitesse de rotation n est exprimée en tours par minute. La fréquence d'excitation en hertz est calculée à partir de la vitesse de rotation. La fréquence d'excitation fErreger en hertz est : f_Erreger = n / 60. La fréquence angulaire ω est :
ω = 2 * π * f_Erreger = 2 * π * n / 60
ω = 2 π n/60
Exemple : pour n = 600 tours par minute, on obtient f_excitation = 10 hertz.
Dans le granulateur mélangeur à couche annulaire, la chambre de mélange est ouverte.
Effets de déséquilibre et force de déséquilibre
Le déséquilibre est décrit par une masse déséquilibrée mu. La masse déséquilibrée mu est située à une distance e de l'axe de rotation. Le déséquilibre subit une force centripète lors de la rotation. L'amplitude de la force de déséquilibre F0 est :
F0 = mu e ω2
La force d'excitation F(t) dépendante du temps peut être considérée comme sinusoïdale. La force d'excitation s'écrit alors comme suit :
F(t) = F0 sin (ω t)
Cette force agit verticalement au centre de la poutre.
Rigidité théorique du ressort au centre du champ
La poutre est considérée comme une poutre à appui simple avec une charge ponctuelle au centre. La portée de la poutre est L. La rigidité à la flexion de la poutre est donnée par le produit E * I. E est le module d'élasticité de l'acier. I est le moment d'inertie de la section. Une force verticale statique F agit au centre de la poutre. La flexion statique δ_stat au centre de la poutre est :
δstat = F L3/ (48 E I)
La rigidité du ressort k_eff est définie comme la force divisée par le déplacement. Une fois appliquée, on obtient :
keff = F / δstat = 48 E I / L3
La rigidité du ressort k_eff décrit la rigidité verticale de la poutre au centre du champ.
Granulateur à couche annulaire.
Masse effective m_eff du système
La masse oscillante est constituée de la masse de la machine et d'une partie de la masse du support. La masse de la machine est m_M. La masse du support est m_B. Toutes les parties du support n'oscillent pas avec la même intensité. C'est pourquoi on utilise un facteur de participation η. Le facteur de participation est souvent compris entre 0,2 et 0,3. Une simplification fréquemment utilisée est η = 0,25. La masse effective m_eff est alors calculée comme la somme :
meff = mM + η mB
Si la masse de la machine est nettement supérieure à la masse du support, on peut approximativement poser m_eff ≈ m_M.
Fréquence propre de l'ensemble du système
Le système est considéré comme un oscillateur à masse unique avec la masse m_eff et la rigidité du ressort k_eff. L'équation différentielle de l'oscillateur à masse unique non amorti est la suivante :
meff x¨(t) + keff x(t) = 0
La fréquence propre ω_0 est :
ω0 = sqrt (keff/meff)
La fréquence propre f_0 en hertz est :
f0 = ω0 / (2π)
f0 = (1 / (2 π)) sqrt (keff / meff)
Si k_eff est remplacé par 48 * E * I / L^3, on obtient :
f0 = (1 / (2 π)) sqrt ((48 E I) / (L3 meff))
Cette formule montre que la fréquence propre augmente avec la rigidité à la flexion E * I et diminue avec la portée L et la masse effective m_eff.
Comparaison entre la fréquence d'excitation et la fréquence propre pour évaluer le risque de résonance
La fréquence d'excitation f_Erreger est calculée à partir de la vitesse de rotation de la machine. La fréquence propre f_0 est calculée à partir de la rigidité du ressort du support et de la masse effective. Il existe un risque de résonance lorsque la fréquence d'excitation est proche de la fréquence propre. La condition de résonance est approximativement la suivante :
fErreger ≈ f0
Pour garantir une conception sûre, il convient de prévoir un écart entre la fréquence propre et la fréquence d'excitation. On choisit souvent comme valeur indicative un écart d'environ 20 % ou plus. Si la fréquence propre est nettement supérieure à la plage de vitesse totale, le risque de résonance est faible. Si la fréquence propre est nettement inférieure à la plage de vitesse totale, le risque de résonance est également faible. Si la fréquence propre se situe dans la plage de vitesse utilisée, un problème de vibration est probable.
Cette déduction permet d'évaluer dans un premier temps si un problème de résonance est à prévoir avec l'agglomérateur à couche annulaire sur un support.
Une fois terminés, les agglomérateurs amixon® sont soumis à un traitement d'équilibrage. Ce traitement permet d'éliminer les déséquilibres statiques et dynamiques. De plus, les machines sont équipées de systèmes d'amortissement. Ceux-ci isolent les vibrations éventuelles des fondations et évitent ainsi le bruit.
© Copyright by amixon GmbH