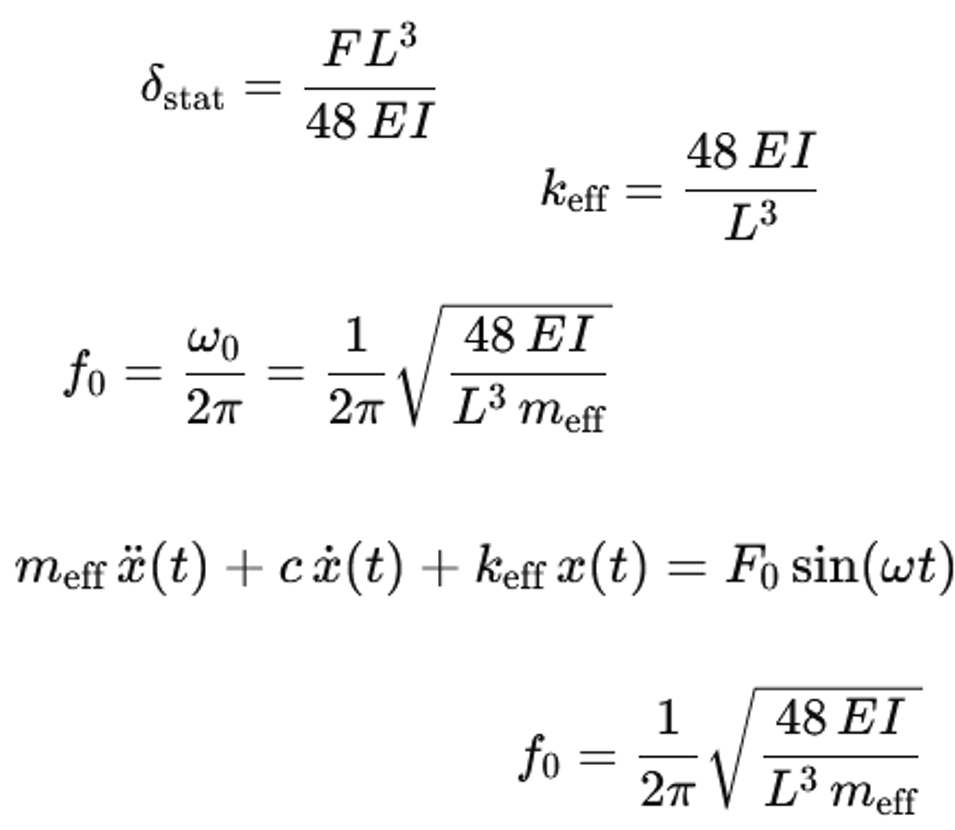Determinare le frequenze di risonanza
Si tratta di una prima valutazione della probabilità che si tratti di un problema di vibrazioni con rischio di risonanza. La seguente deduzione si riferisce a un granulatore miscelatore ad anello amixon®. La situazione è fortemente idealizzata.
Il granulatore misto a strato anulare è montato al centro su un supporto a cuscinetto singolo. È considerato un carico puntuale. Questo poggia a destra e a sinistra su due appoggi come un ponte. La macchina è dotata di un motore di azionamento e di un albero di miscelazione rotante. Il motore e l'albero ruotano a una velocità n [giri al minuto]. L'albero di miscelazione presenta un leggero squilibrio. Questo genera una forza verticale periodica al centro del supporto. Per la stima, il sistema viene modellato come un oscillatore a massa singola. Il supporto viene considerato come una molla con una rigidità keff. La macchina e una parte del supporto vengono considerate come massa effettiva m_(eff). Lo squilibrio genera una forza eccitante armonica F(t). Si devono stimare i seguenti dati:
- frequenza di eccitazione
- Effetti di squilibrio
- rigidità teorica della molla
- Frequenza propria dell'intero sistema
Frequenza di eccitazione dello squilibrio
La velocità di rotazione n è espressa in giri al minuto. La frequenza di eccitazione in hertz viene calcolata dalla velocità di rotazione. La frequenza di eccitazione fErreger in hertz è: f_Erreger = n / 60. La frequenza angolare di eccitazione ω è:
ω = 2 * π * f_Erreger = 2 * π * n / 60
ω = 2 π n/60
Esempio: con n = 600 giri al minuto, si ottiene f_eccitatore = 10 Hertz.
Nel granulatore misto ad anello, la camera di miscelazione è aperta.
Effetti di squilibrio e forza di squilibrio
Lo squilibrio è descritto da una massa di squilibrio mu. La massa di squilibrio mu ha una distanza e dall'asse di rotazione. Lo squilibrio subisce una forza centripeta durante la rotazione. L'ampiezza della forza di squilibrio F0 è:
F0 = mu e ω2
La forza eccitante dipendente dal tempo F(t) può essere considerata sinusoidale. La forza eccitante viene quindi scritta come:
F(t) = F0 sin (ω t)
Questa forza agisce verticalmente al centro della trave.
Rigidità teorica della molla del supporto al centro del campo
La trave è considerata come una trave a semplice appoggio con un carico puntuale al centro. La campata della trave è L. La rigidità alla flessione della trave è data dal prodotto E * I. E è il modulo di elasticità dell'acciaio. I è il momento di inerzia della sezione trasversale. Una forza statica verticale F agisce al centro della trave. La flessione statica δ_stat al centro della trave è:
δstat = F L3/ (48 E I)
La rigidità della molla k_eff è definita come forza divisa per spostamento. Applicata, si ottiene:
keff = F / δstat = 48 E I / L3
La rigidità elastica k_eff descrive la rigidità verticale della trave al centro del campo.
Granulatore a strati circolari.
Massa effettiva m_eff del sistema
La massa oscillante è costituita dalla massa della macchina e da una parte della massa del supporto. La massa della macchina è m_M. La massa del supporto è m_B. Non tutte le parti del supporto oscillano con la stessa intensità. Pertanto, viene utilizzato un fattore di partecipazione η. Il fattore di partecipazione è spesso compreso tra 0,2 e 0,3. Una semplificazione comunemente utilizzata è η = 0,25. La massa effettiva m_eff viene quindi calcolata come somma:
meff = mM + η mB
Se la massa della macchina è notevolmente superiore alla massa del supporto, è possibile impostare approssimativamente m_eff ≈ m_M.
Frequenza propria dell'intero sistema
Il sistema è considerato come un oscillatore a massa singola con massa m_eff e rigidità elastica k_eff. L'equazione differenziale dell'oscillatore a massa singola non smorzato è:
meff x¨(t) + keff x(t) = 0
La frequenza naturale ω_0 è:
ω0 = sqrt (keff/meff)
La frequenza naturale f_0 in Hertz è:
f0 = ω0 / (2π)
f0 = (1 / (2 π)) sqrt (keff / meff)
Sostituendo k_eff con 48 * E * I / L^3, si ottiene:
f0 = (1 / (2 π)) sqrt ((48 E I) / (L3 meff))
Questa formula mostra che la frequenza propria aumenta con la rigidità alla flessione E * I e diminuisce con la campata L e la massa effettiva m_eff.
Confronto tra frequenza di eccitazione e frequenza propria per valutare il rischio di risonanza
La frequenza di eccitazione f_Erreger viene calcolata dalla velocità di rotazione della macchina. La frequenza propria f_0 viene calcolata dalla rigidità elastica del supporto e dalla massa effettiva. Esiste il pericolo di risonanza quando la frequenza di eccitazione è vicina alla frequenza propria. La condizione di risonanza è approssimativamente la seguente:
fErreger ≈ f0
Per garantire una progettazione sicura, è necessario che vi sia una distanza tra la frequenza propria e la frequenza di eccitazione. Spesso si sceglie come valore di riferimento una distanza pari a circa il 20% o superiore. Se la frequenza propria è nettamente superiore all'intero intervallo di velocità, il rischio di risonanza è basso. Se la frequenza propria è nettamente inferiore all'intero intervallo di velocità, anche in questo caso il rischio di risonanza è basso. Se la frequenza propria rientra nell'intervallo di velocità utilizzato, è probabile che si verifichi un problema di vibrazioni.
Questa deduzione consente una prima valutazione per stabilire se sia prevedibile un problema di risonanza nell'agglomeratore misto a strati ad anello su un supporto.
Una volta completati, gli agglomeratori amixon® vengono sottoposti a un trattamento di bilanciamento. In questo modo vengono eliminati sia lo squilibrio statico che quello dinamico. Inoltre, le macchine sono dotate di sistemi di smorzamento che isolano le eventuali vibrazioni dalle fondamenta ed evitano la produzione di rumore.
© Copyright by amixon GmbH