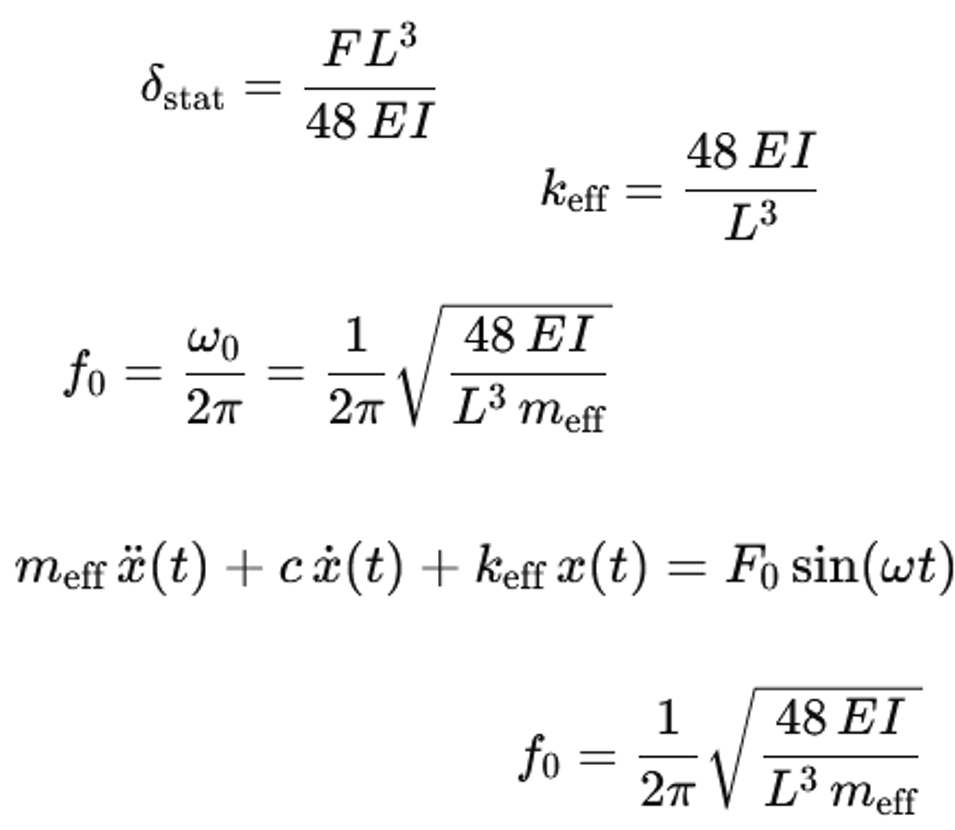공진 주파수 측정

이것은 공진 위험이 있는 진동 문제인지에 대한 초기 확률 평가에 관한 것입니다. 다음 도출은 amixon® 링층 혼합 과립기에 적용됩니다. 해당 상황은 상당히 단순화되었습니다.

링층 혼합 그라눌레이터는 단일 지지대 중앙에 장착되어 있습니다. 이는 점하중으로 간주됩니다. 이 장치는 오른쪽과 왼쪽에 두 개의 지지대에 다리처럼 놓여 있습니다. 기계에는 구동 모터와 회전 혼합 작업축이 있습니다. 모터와 축은 분당 회전수 n [회전/분]으로 회전합니다. 혼합 작업축은 작은 불균형을 가지고 있습니다. 이는 지지대 중앙에 주기적인 수직력을 발생시킵니다. 추정하기 위해 시스템은 단일 질량 진동자로 모델링됩니다. 이때 지지대는 강성 keff을 가진 스프링으로 간주됩니다. 기계와 지지대의 일부는 유효 질량 m_(eff)로 간주됩니다. 불균형은 조화 진동력 F(t)를 발생시킵니다. 다음 데이터를 추정해야 합니다:

자극 주파수
불균형 효과
이론적 스프링 강성
전체 시스템의 고유 진동수

불균형의 유발 주파수

회전수 n은 분당 회전수로 표시됩니다. 회전수로부터 헤르츠 단위의 발전기 주파수가 계산됩니다. 헤르츠 단위의 발전기 주파수 fErreger는 다음과 같습니다: f_Erreger = n / 60. 발전기 고주파 진동수 ω는 다음과 같습니다:

ω = 2 * π * f_Erreger = 2 * π * n / 60

ω = 2 π n/60

예시: n = 600 회전/분일 때, f_자극 = 10 헤르츠가 됩니다.

링층 혼합 그라눌레이터에서는 혼합실이 열려 있습니다.

불균형 효과와 불균형력

불균형은 불균형 질량 μ로 설명된다. 불균형 질량 μ는 회전축으로부터 거리 e를 가진다. 불균형은 회전 시 구심력을 받는다. 불균형력 F0의 진폭은 다음과 같다:

F₀= m_ue ω²

시간에 의존하는 유도력 F(t)는 사인파 형태로 가정할 수 있다. 유도력은 다음과 같이 표현된다:

F(t) = F₀ sin (ω t)

이 힘은 보의 중심에서 수직으로 작용합니다.

보의 중간 부위에서의 이론적 스프링 강성

보(梁)는 중앙에 점하중이 가해지는 단순 지지 보로 간주됩니다. 보의 경간은 L입니다. 보의 굽힘 강성은 E * I의 곱으로 주어집니다. E는 강철의 탄성 계수입니다. I는 단면의 면적 관성 모멘트입니다. 정적 수직 힘 F가 보의 중앙에 작용합니다. 보 중앙의 정적 휨 변형 δ_stat는 다음과 같습니다:

δ_stat = F L³/ (48 E I)

스프링 강성 k_eff는 힘과 변위의 비로 정의됩니다. 이를 적용하면 다음과 같습니다:

k_eff = F / δ_stat = 48 E I / L³

스프링 강성 k_eff는 보의 중간 부위에서의 수직 강성을 나타냅니다.

링층 혼합 그라뉼레이터.

시스템의 유효 질량 m_eff

진동 질량은 기계의 질량과 지지대의 질량 일부로 구성됩니다. 기계의 질량은 m_M입니다. 지지대의 질량은 m_B입니다. 지지대의 모든 부분이 동일한 강도로 진동하는 것은 아닙니다. 따라서 참여 계수 η가 사용됩니다. 참여 계수는 종종 0.2에서 0.3 사이입니다. 흔히 사용되는 단순화 값은 η = 0.25입니다. 그러면 유효 질량 m_eff는 다음과 같이 합계로 설정됩니다:

m_eff= m_M+ η m_B

기계 질량이 지지대 질량보다 현저히 클 경우, 근사적으로 m_eff ≈ m_M으로 설정할 수 있다.

전체 시스템의 고유 진동수

이 시스템은 질량 m_eff와 스프링 강성 k_eff를 가진 단일 질량 진동자로 간주됩니다. 감쇠가 없는 단일 질량 진동자의 미분 방정식은 다음과 같습니다:

m_eff x¨(t) + k_eff x(t) = 0

고유 진동수 ω₀는 다음과 같습니다:

ω₀ = sqrt (k_eff/m_eff)

고유 진동수 f_0 (헤르츠)는 다음과 같습니다:

f₀ = ω₀/ (2π)

f₀ = (1 / (2 π)) sqrt (k_eff / m_eff)

k_eff를 48 * E * I / L^3으로 대체하면 다음과 같이 됩니다:

f₀ = (1 / (2 π)) sqrt ((48 E I) / (L³ m_eff))

이 공식은 고유 진동수가 굽힘 강성 E * I에 비례하고, 경간 L과 유효 질량 m_eff에 반비례함을 보여줍니다.

자극 주파수와 고유 주파수의 비교를 통한 공진 위험성 평가

자극 주파수 f_Erreger는 기계의 회전 속도로부터 계산됩니다. 고유 주파수 f_0는 지지대의 스프링 강성과 유효 질량으로부터 계산됩니다. 자극 주파수가 고유 주파수에 근접할 경우 공진 위험이 존재합니다. 공진 조건은 대략 다음과 같습니다:

f_Erreger ≈ f₀

안전한 설계를 위해서는 고유 진동수와 구동 진동수 사이에 간격이 있어야 합니다. 일반적으로 약 20% 이상의 간격을 기준으로 선택합니다. 고유 진동수가 전체 회전 속도 범위보다 현저히 높으면 공진 위험이 낮습니다. 고유 진동수가 전체 회전 속도 범위보다 현저히 낮으면 공진 위험 역시 낮습니다. 고유 진동수가 사용되는 회전 속도 범위 내에 있으면 진동 문제가 발생할 가능성이 높습니다.

이 유도식은 지지체 상의 링층 혼합 응집기에서 공진 문제가 발생할지 여부에 대한 초기 평가를 가능하게 합니다.

amixon® 응집기는 생산 완료 후 균형 조정 절차를 거칩니다. 이 과정에서 정적 및 동적 불균형이 모두 제거됩니다. 또한 기계는 진동 흡수 장치에 설치되어 발생할 수 있는 진동을 기초로부터 차단하고 소음을 방지합니다.

혼합기