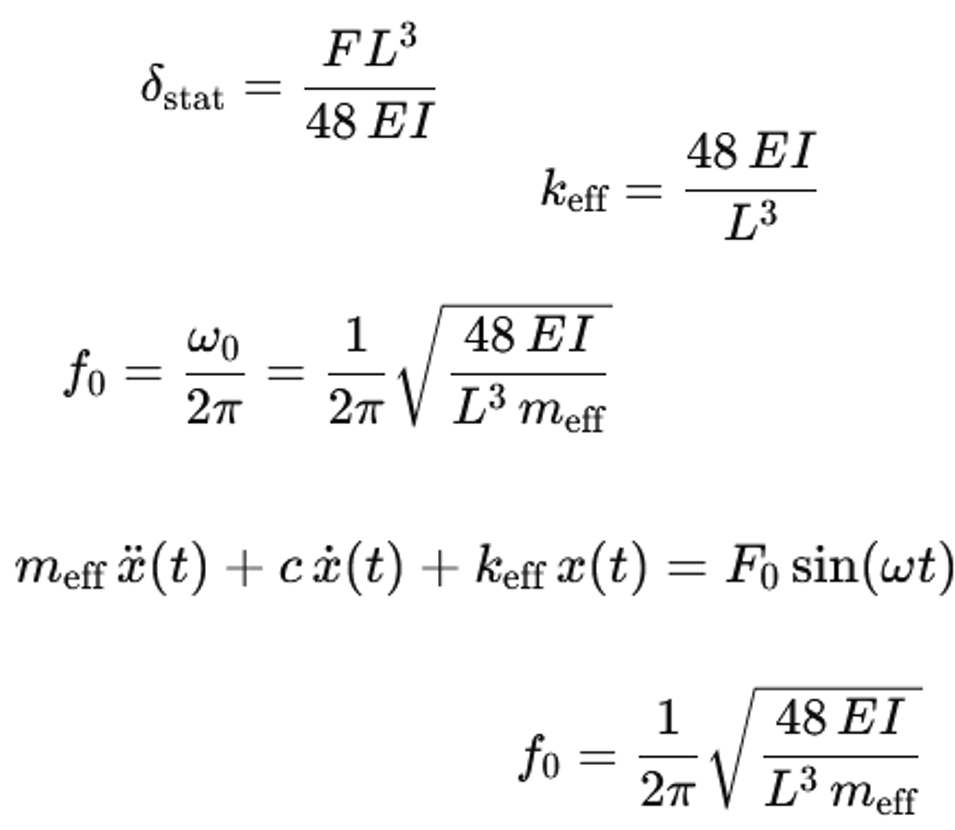Determinar las frecuencias de resonancia
Se trata de una primera estimación de la probabilidad de que se trate de un problema de vibraciones con riesgo de resonancia. La siguiente deducción se refiere a un granulador mezclador de capa anular amixon®. Los hechos están muy idealizados.
El granulador mezclador de capa anular está montado en el centro sobre un soporte de un solo cojinete. Se considera una carga puntual. Esta se apoya a derecha e izquierda como un puente sobre dos soportes. La máquina dispone de un motor de accionamiento y un eje mezclador giratorio. El motor y el eje giran a una velocidad n [revoluciones por minuto]. El eje mezclador tiene un pequeño desequilibrio. Esto genera una fuerza vertical periódica en el centro del soporte. Para la estimación, el sistema se modela como un oscilador de masa única. El soporte se considera un resorte con una rigidez keff. La máquina y una parte del soporte se consideran una masa efectiva m_(eff). El desequilibrio genera una fuerza excitadora armónica F(t). Se deben estimar los siguientes datos:
- frecuencia de excitación
- Efectos de desequilibrio
- rigidez teórica del muelle
- Frecuencia natural del sistema completo
Frecuencia de excitación del desequilibrio
La velocidad de rotación n se indica en revoluciones por minuto. A partir de la velocidad de rotación se calcula la frecuencia de excitación en hercios. La frecuencia de excitación fErreger en hercios es: f_Erreger = n / 60. La frecuencia angular de excitación ω es:
ω = 2 * π * f_Erreger = 2 * π * n / 60
ω = 2 π n/60
Ejemplo: con n = 600 revoluciones por minuto, se obtiene f_excitate = 10 hercios.
En el granulador mezclador de capa anular, la cámara de mezcla está abierta.
Efectos del desequilibrio y fuerza del desequilibrio
El desequilibrio se describe mediante una masa desequilibrada mu. La masa desequilibrada mu tiene una distancia e desde el eje de rotación. El desequilibrio experimenta una fuerza centrípeta durante la rotación. La amplitud de la fuerza de desequilibrio F0 es:
F0 = mu e ω2
La fuerza excitante dependiente del tiempo F(t) puede considerarse sinusoidal. La fuerza excitante se escribe entonces como:
F(t) = F0 sin (ω t)
Esta fuerza actúa verticalmente en el centro del soporte.
Rigidez teórica del muelle del soporte en el centro del campo
La viga se considera una viga simple con una carga puntual en el centro. La luz de la viga es L. La rigidez a la flexión de la viga viene dada por el producto E * I. E es el módulo de elasticidad del acero. I es el momento de inercia de la sección transversal. Una fuerza vertical estática F actúa en el centro de la viga. La flexión estática δ_stat en el centro de la viga es:
δstat = F L3/ (48 E I)
La rigidez del muelle k_eff se define como la fuerza dividida por el desplazamiento. Al aplicarla, se obtiene:
keff = F / δstat = 48 E I / L3
La rigidez elástica k_eff describe la rigidez vertical del soporte en el centro del campo.
Granulador de mezcla de capa anular.
Masa efectiva m_eff del sistema
La masa oscilante está compuesta por la masa de la máquina y una parte de la masa del soporte. La masa de la máquina es m_M. La masa del soporte es m_B. No todas las partes del soporte vibran con la misma intensidad. Por lo tanto, se utiliza un factor de participación η. El factor de participación suele estar entre 0,2 y 0,3. Una simplificación que se utiliza con frecuencia es η = 0,25. La masa efectiva m_eff se calcula entonces como la suma:
meff = mM + η mB
Si la masa de la máquina es considerablemente mayor que la masa del soporte, se puede establecer aproximadamente m_eff ≈ m_M.
Frecuencia natural del sistema completo
El sistema se considera un oscilador de masa única con la masa m_eff y la rigidez del muelle k_eff. La ecuación diferencial del oscilador de masa única sin amortiguación es:
meff x¨(t) + keff x(t) = 0
La frecuencia natural ω_0 es:
ω0 = sqrt (keff/meff)
La frecuencia propia f_0 en hercios es:
f0 = ω0 / (2π)
f0 = (1 / (2 π)) sqrt (keff / meff)
Si se sustituye k_eff por 48 * E * I / L^3, se obtiene:
f0 = (1 / (2 π)) sqrt ((48 E I) / (L3 meff))
Esta fórmula muestra que la frecuencia propia aumenta con la rigidez a la flexión E * I y disminuye con la luz L y la masa efectiva m_eff.
Comparación entre la frecuencia del excitador y la frecuencia propia para evaluar el riesgo de resonancia.
La frecuencia de excitación f_Erreger se calcula a partir de la velocidad de giro de la máquina. La frecuencia propia f_0 se calcula a partir de la rigidez elástica del soporte y la masa efectiva. Existe riesgo de resonancia cuando la frecuencia de excitación es cercana a la frecuencia propia. La condición de resonancia es aproximadamente:
fErreger ≈ f0
Para garantizar un diseño seguro, debe existir una diferencia entre la frecuencia propia y la frecuencia del excitador. A menudo se elige como valor orientativo una diferencia de aproximadamente el 20 % o más. Si la frecuencia propia es claramente superior al rango de revoluciones total, el riesgo de resonancia es bajo. Si la frecuencia propia es claramente inferior al rango de revoluciones total, el riesgo de resonancia también es bajo. Si la frecuencia propia se encuentra dentro del rango de revoluciones utilizado, es probable que se produzca un problema de vibraciones.
Esta deducción permite realizar una primera estimación sobre si cabe esperar un problema de resonancia en el aglomerador mixto de capa anular sobre un soporte.
Una vez terminados, los aglomeradores de amixon® se someten a un tratamiento de equilibrado. De este modo se eliminan tanto los desequilibrios estáticos como los dinámicos. Además, las máquinas están montadas sobre sistemas de amortiguación. Estos desacoplan las posibles vibraciones de los cimientos y evitan el ruido.
© Copyright by amixon GmbH