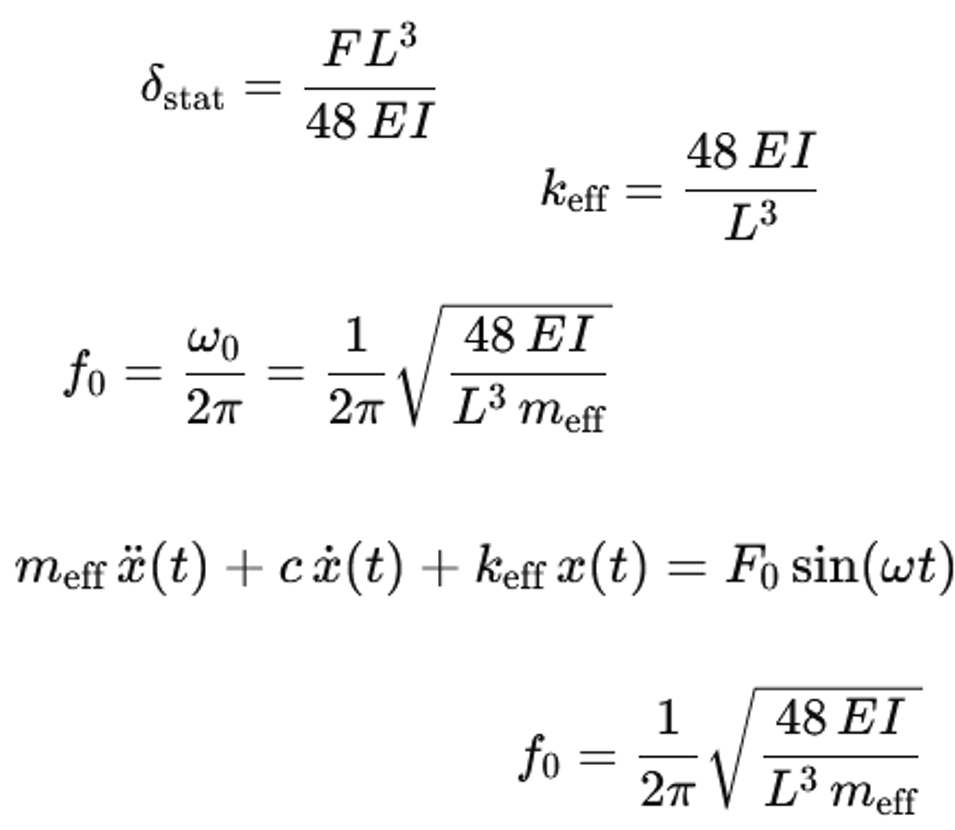Określanie częstotliwości rezonansowych
Chodzi o wstępną ocenę prawdopodobieństwa, czy mamy tu do czynienia z problemem drgań z ryzykiem rezonansu. Poniższe wywody odnoszą się do granulatora mieszającego z warstwą pierścieniową amixon®. Opisana sytuacja jest w dużym stopniu idealizowana.
Granulator mieszający z warstwą pierścieniową jest zamontowany pośrodku na prostym łożysku. Jest on traktowany jako obciążenie punktowe. Znajduje się on po prawej i lewej stronie, podobnie jak most, na dwóch podporach. Maszyna posiada silnik napędowy i obrotowy wał mieszający. Silnik i wał obracają się z prędkością n [obrotów na minutę]. Wał mieszający ma niewielkie niewyważenie. Powoduje to powstanie okresowej siły pionowej w środku wspornika. W celu oszacowania system modeluje się jako oscylator jednokorpusowy. Wspornik traktuje się jako sprężynę o sztywności keff. Maszyna i część wspornika traktowane są jako masa efektywna m_(eff). Wyważenie powoduje powstanie harmonicznej siły wzbudzającej F(t). Należy oszacować następujące dane:
- częstotliwość pobudzająca
- Efekty niewyważenia
- teoretyczna sztywność sprężyny
- Własna częstotliwość całego systemu
Częstotliwość wzbudzająca niewyważenia
Prędkość obrotowa n jest podawana w obrotach na minutę. Na podstawie prędkości obrotowej oblicza się częstotliwość wzbudzenia w hercach. Częstotliwość wzbudzenia fErreger w hercach wynosi: f_Erreger = n / 60. Częstotliwość obwodowa wzbudzenia ω wynosi:
ω = 2 * π * f_Erreger = 2 * π * n / 60
ω = 2 π n/60
Przykład: Przy n = 600 obrotów na minutę otrzymujemy f_Erreger = 10 herców.
W mieszalniku pierścieniowym komora mieszania jest otwarta.
Efekty niewyważenia i siła niewyważenia
Niewyważenie jest opisane przez masę niewyważenia mu. Masa niewyważenia mu znajduje się w odległości e od osi obrotu. Podczas obrotu niewyważenie podlega sile dośrodkowej. Amplituda siły niewyważenia F0 wynosi:
F0 = mu e ω2
Siłę wzbudzającą zależną od czasu F(t) można przyjąć jako sinusoidalną. Siłę wzbudzającą zapisuje się wówczas jako:
F(t) = F0 sin (ω t)
Siła ta działa pionowo w środku belki.
Teoretyczna sztywność sprężyny belki w środkowej części pola
Belka jest traktowana jako belka o prostym podparciu z obciążeniem punktowym w środku. Rozpiętość belki wynosi L. Sztywność belki na zginanie jest określona przez iloczyn E * I. E jest modułem sprężystości stali. I jest momentem bezwładności przekroju poprzecznego. W środku belki działa statyczna siła pionowa F. Statyczne ugięcie δ_stat w środku belki wynosi:
δstat = F L3/ (48 E I)
Sztywność sprężyny k_eff definiuje się jako iloraz siły i przemieszczenia. Zastosowanie tego wzoru daje następujący wynik:
keff = F / δstat = 48 E I / L3
Sztywność sprężyny k_eff opisuje sztywność pionową belki w środku pola.
Granulator mieszający z warstwą pierścieniową.
Masa efektywna m_eff układu
Masa drgająca składa się z masy maszyny i części masy nośnika. Masa maszyny wynosi m_M. Masa nośnika wynosi m_B. Nie wszystkie części nośnika drgają z taką samą siłą. Dlatego stosuje się współczynnik udziału η. Współczynnik udziału wynosi często od 0,2 do 0,3. Często stosowanym uproszczeniem jest η = 0,25. Masę efektywną m_eff oblicza się wówczas jako sumę:
meff = mM + η mB
Jeśli masa maszyny jest znacznie większa niż masa nośnika, można przyjąć przybliżoną wartość m_eff ≈ m_M.
Własna częstotliwość całego systemu
Układ traktowany jest jako oscylator jednokmasowy o masie m_eff i sztywności sprężyny k_eff. Równanie różniczkowe oscylatora jednokmasowego bez tłumienia ma postać:
meff x¨(t) + keff x(t) = 0
Częstotliwość własna ω_0 wynosi:
ω0 = sqrt (keff/meff)
Częstotliwość drgań własnych f₀ (w hercach) jest następująca.
f0 = ω0 / (2π)
f0 = (1 / (2 π)) sqrt (keff / meff)
Zastąpienie k_eff przez 48 * E * I / L^3 daje następujące równanie.
f0 = (1 / (2 π)) sqrt ((48 E I) / (L3 meff))
Równanie to pokazuje, że częstotliwość drgań własnych jest proporcjonalna do sztywności na zginanie E * I i odwrotnie proporcjonalna do rozpiętości L i masy efektywnej m_eff.
Porównanie częstotliwości wzbudzenia i częstotliwości drgań własnych w celu oceny ryzyka rezonansu
Częstotliwość wzbudzenia f_Erreger jest obliczana na podstawie prędkości obrotowej maszyny. Częstotliwość drgań własnych f_0 jest obliczana na podstawie stałej sprężystości belki i masy efektywnej. Gdy częstotliwość wzbudzenia jest zbliżona do częstotliwości drgań własnych, istnieje ryzyko wystąpienia rezonansu. Warunki rezonansu są w przybliżeniu następujące.
fErreger ≈ f0
Aby zapewnić bezpieczeństwo konstrukcji, należy zapewnić odpowiednią różnicę między częstotliwością drgań własnych a częstotliwością wzbudzenia. W wielu przypadkach jako wartość odniesienia przyjmuje się różnicę wynoszącą około 20% lub więcej. Gdy częstotliwość drgań własnych znacznie przekracza cały zakres prędkości obrotowej, ryzyko rezonansu jest niskie. Podobnie, gdy częstotliwość drgań własnych znacznie spada poniżej całego zakresu prędkości obrotowej, ryzyko rezonansu jest niskie. Jeśli częstotliwość drgań własnych mieści się w zakresie prędkości obrotowej roboczej, prawdopodobieństwo wystąpienia problemów z drganiami wzrasta.
Wynik ten umożliwia wstępną ocenę, czy w przypadku hybrydowego agregatora warstwy pierścieniowej na nośniku pojawiają się problemy związane z rezonansem.
Po zakończeniu produkcji aglomeratory firmy amixon® poddawane są procesowi wyważania. Eliminuje to zarówno niewyważenie statyczne, jak i dynamiczne. Ponadto maszyny są wyposażone w systemy tłumiące. Oddzielają one ewentualne drgania od fundamentów i zapobiegają hałasowi.
© Copyright by amixon GmbH