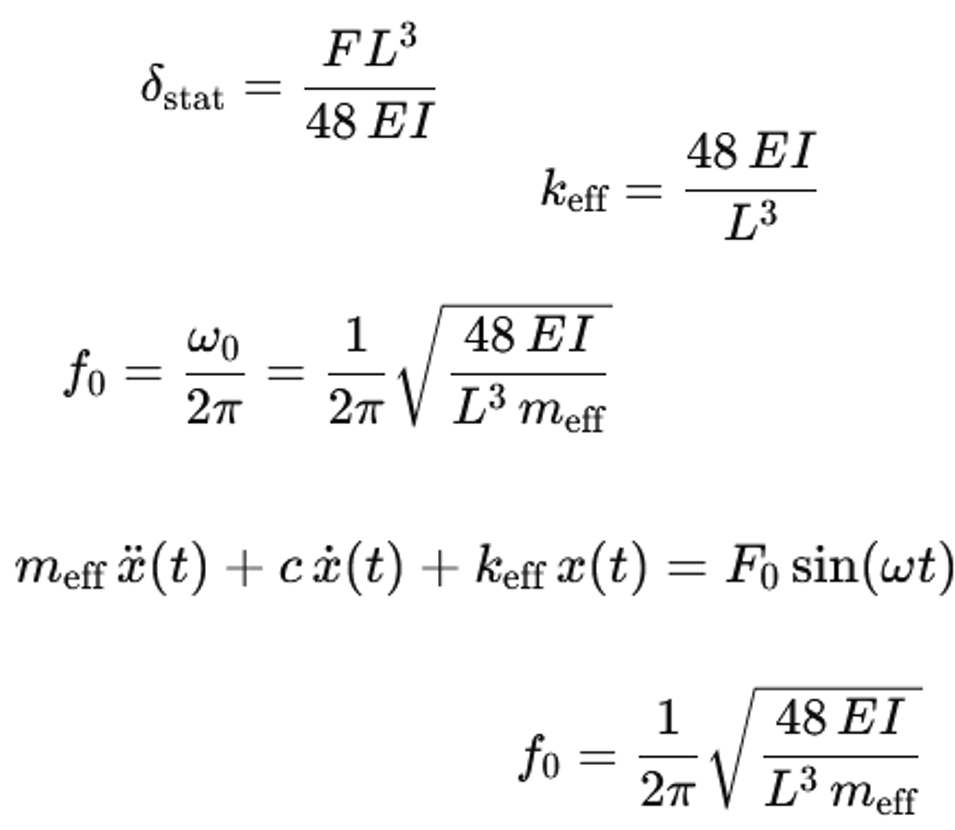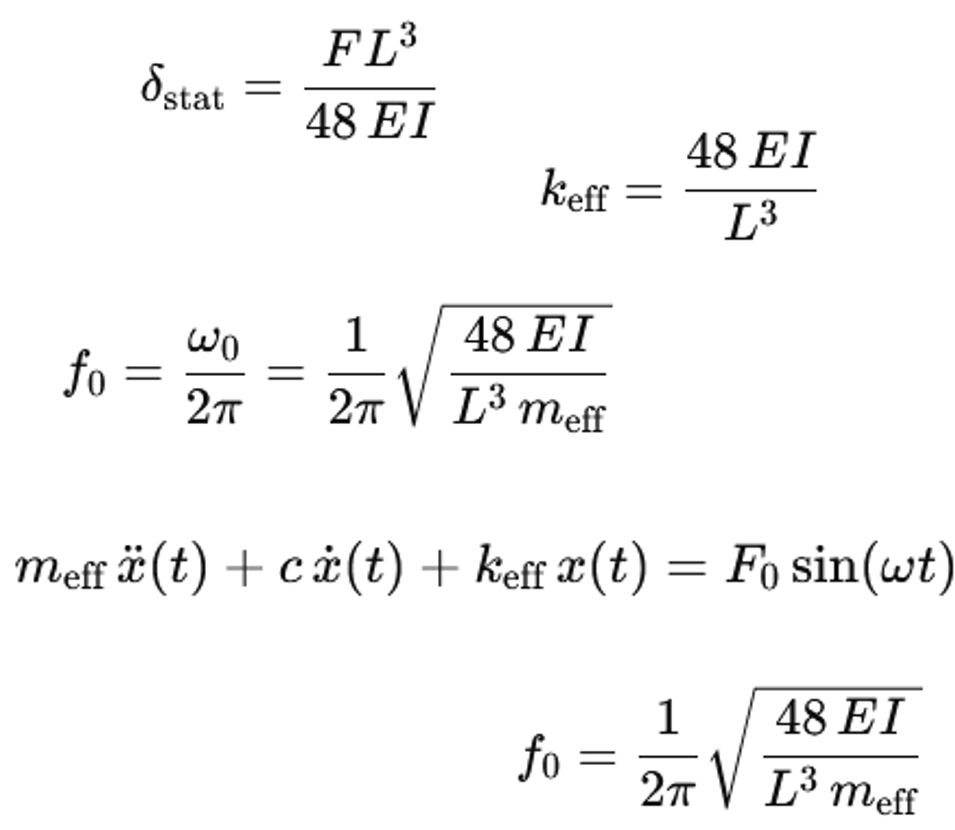Resonanzfrequenzen ermitteln
Es geht um eine erste Abschätzung der Wahrscheinlichkeit, ob es sich hierbei um ein Schwingungsproblem mit Resonanzgefahr handelt. Die folgende Herleitung bezieht sich auf einen amixon® Ringschicht-Mischgranulator. Der Sachverhalt ist stark idealisiert.
Der Ringschicht-Mischgranulator ist mittig auf einem einfach gelagerten Träger montiert. Er wird als Punktlast betrachtet. Dieser liegt rechts und links wie eine Brücke auf zwei Auflagern auf. Die Maschine verfügt über einen Antriebsmotor und eine rotierende Mischwerkwelle. Motor und Welle drehen sich mit einer Drehzahl n [Umdrehungen pro Minute]. Die Mischwerkwelle hat eine kleine Unwucht. Diese erzeugt eine periodische vertikale Kraft in der Trägermitte. Zur Abschätzung wird das System als Einmassenschwinger modelliert. Der Träger wird dabei als Feder mit einer Federsteifigkeit keff betrachtet. Die Maschine und ein Anteil des Trägers werden als effektive Masse m_(eff) betrachtet. Die Unwucht erzeugt eine harmonische Erregerkraft F(t). Folgende Daten sollen abgeschätzt werden:
- Erregerfrequenz
- Unwuchteffekte
- theoretische Federsteifigkeit
- Eigenfrequenz des Gesamtsystems
Erregerfrequenz der Unwucht
Die Drehzahl n wird in Umdrehungen pro Minute angegeben. Aus der Drehzahl wird die Erregerfrequenz in Hertz berechnet. Die Erregerfrequenz fErreger in Hertz ist: f_Erreger = n / 60. Die Erregerkreisfrequenz ω ist:
ω = 2 * π * f_Erreger = 2 * π * n / 60
ω = 2 π n/60
Beispiel: Bei n = 600 Umdrehungen pro Minute ergibt sich f_Erreger = 10 Hertz.
Beim Ringschicht-Mischgranulator ist der Mischraum aufgeklappt.
Unwuchteffekte und Unwuchtkraft
Die Unwucht wird durch eine Unwuchtmasse mu beschrieben. Die Unwuchtmasse mu hat einen Abstand e von der Drehachse. Die Unwucht erfährt bei Rotation eine Zentripetalkraft. Die Amplitude der Unwuchtkraft F0 ist:
F0 = mu e ω2
Die zeitabhängige Erregerkraft F(t) kann als sinusförmig angenommen werden. Die Erregerkraft wird dann geschrieben als:
F(t) = F0 sin (ω t)
Diese Kraft wirkt vertikal in der Mitte des Trägers.
Theoretische Federsteifigkeit des Trägers in Feldmitte
Der Träger wird als einfach gelagerter Balken mit einer Punktlast in der Mitte betrachtet. Die Spannweite des Trägers ist L. Die Biegesteifigkeit des Trägers ist durch das Produkt E * I gegeben. E ist der Elastizitätsmodul des Stahls. I ist das Flächenträgheitsmoment des Querschnittes. Eine statische vertikale Kraft F wirkt in der Mitte des Trägers. Die statische Durchbiegung δ_stat in der Mitte des Trägers ist:
δstat = F L3/ (48 E I)
Die Federsteifigkeit k_eff ist definiert als Kraft geteilt durch Verschiebung. Eingesetzt ergibt sich:
keff = F / δstat = 48 E I / L3
Die Federsteifigkeit k_eff beschreibt die vertikale Steifigkeit des Trägers in Feldmitte.
Ringschicht Mischgranulator.
Effektive Masse m_eff des Systems
Die schwingende Masse besteht aus der Masse der Maschine und einem Anteil der Trägermasse. Die Masse der Maschine ist m_M. Die Masse des Trägers ist m_B. Nicht alle Teile des Trägers schwingen gleich stark. Daher wird ein Beteiligungsfaktor η verwendet. Der Beteiligungsfaktor liegt oft zwischen 0,2 und 0,3. Eine häufig verwendete Vereinfachung ist η = 0,25. Die effektive Masse m_eff wird dann als Summe angesetzt:
meff = mM + η mB
Wenn die Maschinenmasse deutlich größer ist als die Trägermasse, kann näherungsweise m_eff ≈ m_M gesetzt werden.
Eigenfrequenz des Gesamtsystems
Das System wird als Einmassenschwinger mit der Masse m_eff und der Federsteifigkeit k_eff betrachtet. Die Differentialgleichung des ungedämpften Einmassenschwingers lautet:
meff x¨(t) + keff x(t) = 0
Die Eigenkreisfrequenz ω_0 ist:
ω0 = sqrt (keff/meff)
Die Eigenfrequenz f_0 in Hertz ist:
f0 = ω0 / (2π)
f0 = (1 / (2 π)) sqrt (keff / meff)
Wenn k_eff durch 48 * E * I / L^3 ersetzt wird, ergibt sich:
f0 = (1 / (2 π)) sqrt ((48 E I) / (L3 meff))
Diese Formel zeigt, dass die Eigenfrequenz mit der Biegesteifigkeit E * I und abnimmt mit der Spannweite L und der effektiven Masse m_eff.
Vergleich von Erregerfrequenz und Eigenfrequenz zur Abschätzung der Resonanzgefahr
Die Erregerfrequenz f_Erreger wird aus der Drehzahl der Maschine berechnet. Die Eigenfrequenz f_0 wird aus der Federsteifigkeit des Trägers und der effektiven Masse berechnet. Eine Resonanzgefahr besteht, wenn die Erregerfrequenz nahe an der Eigenfrequenz liegt. Die Resonanzbedingung lautet näherungsweise:
fErreger ≈ f0
Zur sicheren Auslegung sollte ein Abstand zwischen Eigenfrequenz und Erregerfrequenz vorhanden sein. Oft wird als Richtwert ein Abstand von etwa 20 Prozent oder mehr gewählt. Liegt die Eigenfrequenz deutlich über dem gesamten Drehzahlbereich, ist die Resonanzgefahr gering. Liegt die Eigenfrequenz deutlich unter dem gesamten Drehzahlbereich, ist die Resonanzgefahr ebenfalls gering. Liegt die Eigenfrequenz innerhalb des genutzten Drehzahlbereiches, ist ein Schwingungsproblem wahrscheinlich.
Diese Herleitung erlaubt eine erste Abschätzung, ob bei dem Ringschicht-Mischagglomerator auf einem Träger ein Resonanzproblem zu erwarten ist.
Nach der Fertigstellung werden Agglomeratoren von amixon® einer Auswuchtbehandlung unterzogen. Dabei werden sowohl statische als auch dynamische Unwucht beseitigt. Darüber hinaus stehen die Maschinen auf Dämpfungssystemen. Diese entkoppeln etwaig auftretende Vibrationen vom Fundament und vermeiden Lärm.
© Copyright by amixon GmbH