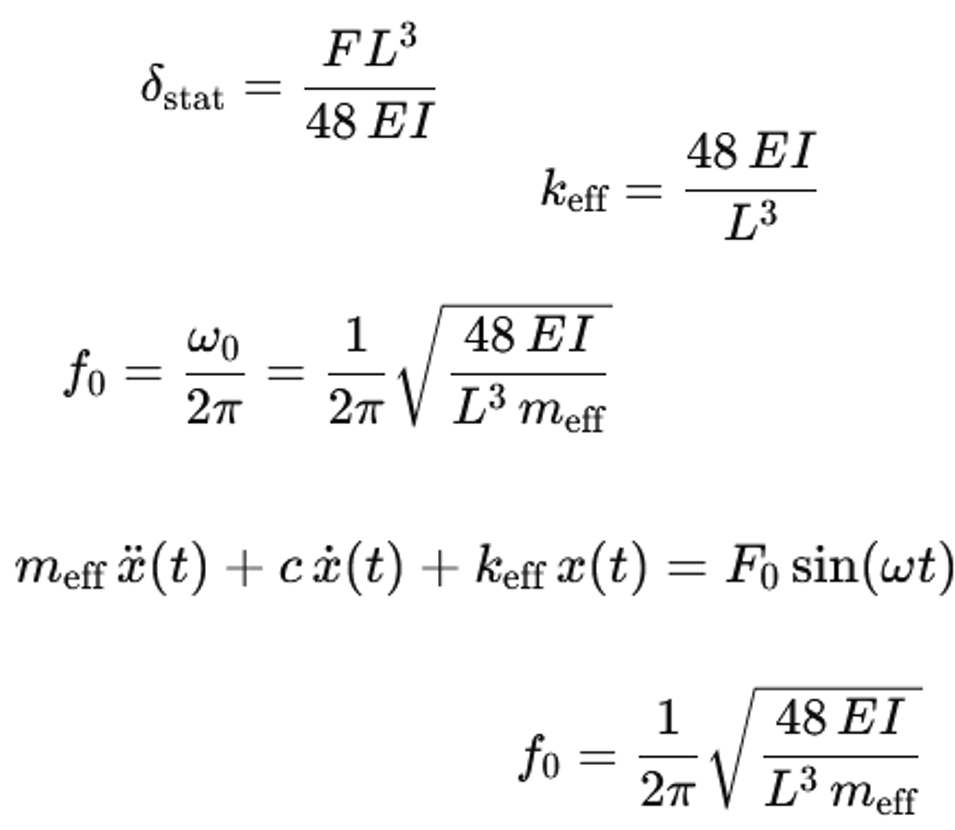
Unwuchtkorrektur bei rotierenden Wellen

Fallbeispiel: Eine horizontal rotierende Welle wird a) statisch und b) dynamisch durch gezieltes Hinzufügen oder Entfernen von Masse in definierten Ebenen so korrigiert, dass die resultierende Unwuchtkraft bzw. das Unwuchtmoment verschwindet oder unter eine Toleranz sinkt. Statisches Wuchten korrigiert eine reine Schwerpunktverschiebung in einer Ebene, dynamisches Wuchten korrigiert zusätzlich kippende Unwuchtanteile durch Ausgleich in zwei (oder mehr) Ebenen entlang der Welle.

1. Unwucht und Erregerfrequenz

Eine rotierende Welle mit Unwucht wird durch eine exzentrische Masse beschrieben. Diese Unwuchtmasse hat die Größe m_u und den Abstand e von der Drehachse. Das Unwuchtprodukt ist U=m_u e. Die Welle dreht mit der Drehzahl n in Umdrehungen pro Minute. Daraus ergibt sich die Erregerfrequenz in Hertz zu f=n/60. Die zugehörige Winkelgeschwindigkeit ist Ω=2πf=2πn/60.

Die Unwuchtmasse bewegt sich auf einer Kreisbahn und erfährt eine radiale Fliehkraft. Der Betrag dieser Kraft ist F_u=m_u eΩ^2=UΩ^2. Für die Schwingungsanregung interessiert die Projektion dieser Kraft in eine feste Richtung, zum Beispiel vertikal. Diese Projektion ändert sich harmonisch mit der Zeit. Daher schreibt man die zeitabhängige Erregerkraft als

F(t)=F_0 sin⁡(Ωt)

Die Amplitude F_0 ist gleich m_u e〖 Ω〗^2.

2. Statisches Wuchten

Beim statischen Wuchten betrachtet man eine im Wesentlichen kurze, massive Welle. Die Unwucht ist dann als reine statische Unwucht modellierbar. Man lagert die Welle sehr leichtgängig und lässt sie auspendeln. Die schwerste Stelle kommt nach unten und markiert die Richtung des Schwerpunkts. Ziel ist, die Unwucht so zu korrigieren, dass der Schwerpunkt wieder auf der Drehachse liegt.

Bringt man ein Korrekturgewicht m_K in einem Radius r_K an, so muss dessen Unwuchtprodukt das ursprüngliche ausgleichen. Es gilt

m_K r_K=m_u e

Praktisch kann man entweder in der schweren Zone Material abtragen oder gegenüber ein Gewicht anbringen. Nach erfolgreicher Korrektur bleibt die Welle in jeder Winkelstellung stehen und zeigt kein Auspendeln mehr.

3. Dynamisches Wuchten

Beim dynamischen Wuchten berücksichtigt man zusätzlich Momentenunwucht. Dazu werden zwei Korrekturebenen entlang der Welle verwendet. In jeder Ebene kann ein Korrekturgewicht mit bestimmter Masse und Winkelposition angebracht werden. Die Welle läuft auf einer Wuchtmaschine oder im eingebauten Zustand mit niedriger Drehzahl. An den Lagern werden Schwingungen und Phasenlagen gemessen.

Die gemessenen Schwingungsvektoren werden mit Testgewichten in den beiden Ebenen variiert. Aus den Änderungen ergibt sich ein lineares Gleichungssystem, das den Einfluss der Korrekturmassen beschreibt. Dieses System liefert die optimalen Korrekturmassen m_K1 und m_K2 sowie deren Winkelpositionen. Nach dem Anbringen der Korrekturgewichte sind sowohl Kraftunwucht als auch Momentenunwucht stark reduziert, und die Welle läuft bei Betriebsdrehzahl ruhiger.

4. Federsteifigkeit des Trägers

Für die Schwingungsberechnung wird die Welle oft durch ein Ersatzsystem mit einer Masse und einer Feder beschrieben. Die vertikale Steifigkeit eines einfach gelagerten Balkens mit Spannweite L und Biegesteifigkeit EI wird über die statische Durchbiegung bestimmt. Man betrachtet eine Einzellast F in der Balkenmitte. Die Durchbiegung in der Mitte ist

δ=(FL^3)/48EI

Die effektive Federsteifigkeit in der Mitte ergibt sich als k=F/δ. Damit erhält man

k=48EI/L^3 

5. Effektive Masse und Eigenfrequenz

Die schwingende Masse setzt sich aus der Maschinenmasse und einem Anteil der Balkenmasse zusammen. Man definiert eine effektive Masse m_eff. Diese ist näherungsweise m_eff=m_M+ηm_B. Hier ist m_M die Masse der Maschine und m_B die Masse des Trägers. Der Beteiligungsfaktor η liegt typischerweise in einem Bereich von etwa 0,2 bis 0,3. Ist die Maschine sehr viel schwerer als der Träger, setzt man näherungsweise m_eff≈m_M.

Das System aus Federsteifigkeit k und Masse m_eff bildet einen Einmassenschwinger. Die Bewegungsgleichung ohne Dämpfung lautet

m_eff  x ¨(t)+kx(t)=0

Aus dieser Gleichung folgt die Eigenkreisfrequenz

ω_0=√(k/m_eff )

Die Eigenfrequenz in Hertz lautet

f_0=ω_0/2π

Setzt man für den Balken k=48EI/L^3 ein, ergibt sich

f_0=1/2π √(48EI/(L^3 m_eff ))

Diese Beziehung zeigt, dass die Eigenfrequenz mit der Biegesteifigkeit zunimmt und mit wachsender Spannweite und wachsender Masse abnimmt.

6. Resonanzbetrachtung

Zum Abgleich der Resonanzgefahr vergleicht man die Erregerfrequenz der Unwucht mit der Eigenfrequenz. Die Erregerfrequenz ist f=n/60. Die Eigenfrequenz ist f_0. Liegen beide Größen nahe beieinander, ist mit Resonanz zu rechnen. Liegt f deutlich unter oder deutlich über f_0, ist die Resonanzgefahr geringer. In der Praxis wird ein Sicherheitsabstand vorgesehen, damit der Resonanzbereich nicht im Dauerbetrieb liegt.