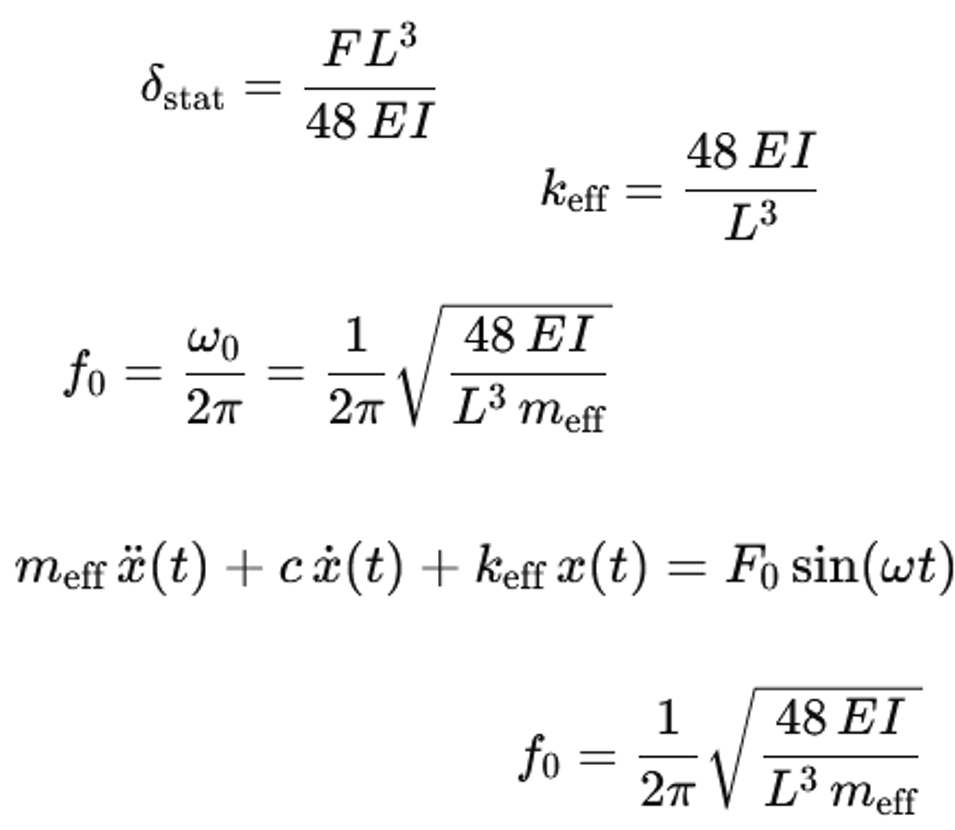
회전축의 불균형 보정

사례 연구: 수평 회전하는 축은 a) 정적 및 b) 동적으로 특정 평면에서 질량을 추가하거나 제거함으로써 교정되어 결과적인 불균형 힘 또는 불균형 모멘트가 사라지거나 허용 오차 이하로 감소합니다. 정적 밸런싱은 단일 평면에서의 순수한 중심 이동을 보정하는 반면, 동적 밸런싱은 추가로 축을 따라 두 개(또는 그 이상)의 평면에서 균형을 맞추어 기울어지는 불균형 요소를 보정합니다.

1. 불균형과 발생 주파수

불균형이 있는 회전축은 편심 질량으로 설명됩니다. 이 불균형 질량은 질량 m_u와 회전축으로부터의 거리 e를 가집니다. 불균형 곱은 U=m_u e입니다. 축은 분당 회전수 n으로 회전합니다. 이로부터 발생하는 진동 주파수는 헤르츠 단위로 f=n/60입니다. 이에 상응하는 각속도는 Ω=2πf=2πn/60입니다.

불균형 질량은 원형 궤도를 따라 움직이며 방사형 원심력을 받는다. 이 힘의 크기는 F_u=m_u eΩ^2=UΩ^2이다. 진동 유발에 있어서는 이 힘이 특정 방향, 예를 들어 수직 방향으로 투영된 값이 중요하다. 이 투영값은 시간에 따라 조화적으로 변화한다. 따라서 시간에 의존하는 유발력은 다음과 같이 표현한다.

F(t)=F_0 sin⁡(Ωt)

진폭 F₀는 m_u e〖 Ω〗^2와 같다.

2. 정적 밸런싱

정적 균형 조정에서는 기본적으로 짧고 단단한 축을 고려합니다. 이때 불균형은 순수한 정적 불균형으로 모델링할 수 있습니다. 축을 매우 부드럽게 지지하고 진동이 멈출 때까지 기다립니다. 가장 무거운 부분이 아래로 내려와 중심점의 방향을 표시합니다. 목표는 불균형을 교정하여 중심점이 다시 회전축 위에 위치하도록 하는 것입니다.

교정추 m_K를 반경 r_K에 부착할 경우, 그 불균형 곱은 원래의 불균형을 상쇄해야 한다. 다음이 성립한다.

m_K r_K=m_u e

실제로는 무거운 구역에서 재료를 제거하거나 반대편에 추를 부착할 수 있습니다. 성공적인 보정 후에는 축이 모든 각도 위치에서 정지 상태를 유지하며 더 이상 흔들림을 보이지 않습니다.

3. 동적 균형 조정

동적 균형 조정 시에는 추가로 모멘트 불균형을 고려합니다. 이를 위해 축을 따라 두 개의 보정 평면을 사용합니다. 각 평면에는 특정 질량과 각도 위치를 가진 보정 중량을 부착할 수 있습니다. 축은 균형 조정 기계 위에서 또는 설치된 상태에서 저속으로 회전합니다. 베어링에서 진동과 위상 위치를 측정합니다.

측정된 진동 벡터는 두 평면에서 시험 중량으로 변화됩니다. 이러한 변화로부터 교정 질량의 영향을 설명하는 선형 방정식 시스템이 도출됩니다. 이 시스템은 최적의 교정 질량 m_K1 및 m_K2와 그 각도 위치를 제공합니다. 보정 중량을 부착한 후에는 힘 불균형과 모멘트 불균형이 모두 크게 감소하며, 샤프트는 작동 회전수에서 더 안정적으로 회전합니다.

4. 지지대의 스프링 강성

진동 계산을 위해 파동은 종종 질량과 스프링으로 구성된 대용 시스템으로 설명됩니다. 단일 지지된 보의 수직 강성은 스팬 L과 굽힘 강성 EI를 통해 정적 휨을 통해 결정됩니다. 보 중앙에 단일 하중 F가 가해지는 경우를 고려합니다. 중앙의 휨은

δ=(FL^3)/48EI

중심에서의 유효 스프링 강성은 k=F/δ로 구해집니다. 이를 통해 다음과 같이 얻어집니다.

k=48EI/L^3 

5. 유효 질량과 고유 진동수

진동 질량은 기계 질량과 빔 질량의 일부로 구성됩니다. 유효 질량 m_eff를 정의합니다. 이는 근사적으로 m_eff=m_M+ηm_B입니다. 여기서 m_M은 기계의 질량이고 m_B는 지지대의 질량입니다. 참여 계수 η는 일반적으로 약 0.2에서 0.3 사이의 범위에 있습니다. 기계가 지지대보다 훨씬 무거울 경우, 근사적으로 m_eff≈m_M으로 설정합니다.

스프링 강성 k와 질량 m_eff로 구성된 시스템은 단일 질량 진동자를 형성한다. 감쇠가 없는 운동 방정식은 다음과 같다.

m_eff  x ¨(t)+kx(t)=0

이 방정식으로부터 고유 원주 주파수가 도출된다.

ω_0=√(k/m_eff )

고유 진동수는 헤르츠 단위로

f_0=ω_0/2π

k=48EI/L^3을 보강재에 대입하면 다음과 같은 결과가 나온다.

f_0=1/2π √(48EI/(L^3 m_eff ))

이 관계는 고유 진동수가 굽힘 강성에 비례하여 증가하고, 스팬과 질량이 증가함에 따라 감소함을 보여준다.

6. 공명 분석

공진 위험을 평가하기 위해 불균형의 자극 주파수와 고유 주파수를 비교합니다. 자극 주파수는 f=n/60입니다. 고유 주파수는 f_0입니다. 두 값이 서로 가까우면 공진이 발생할 가능성이 높습니다. f가 f_0보다 현저히 낮거나 높으면 공진 위험이 낮습니다. 실제 적용 시에는 공진 영역이 연속 운전 중에 발생하지 않도록 안전 여유를 두어야 합니다.