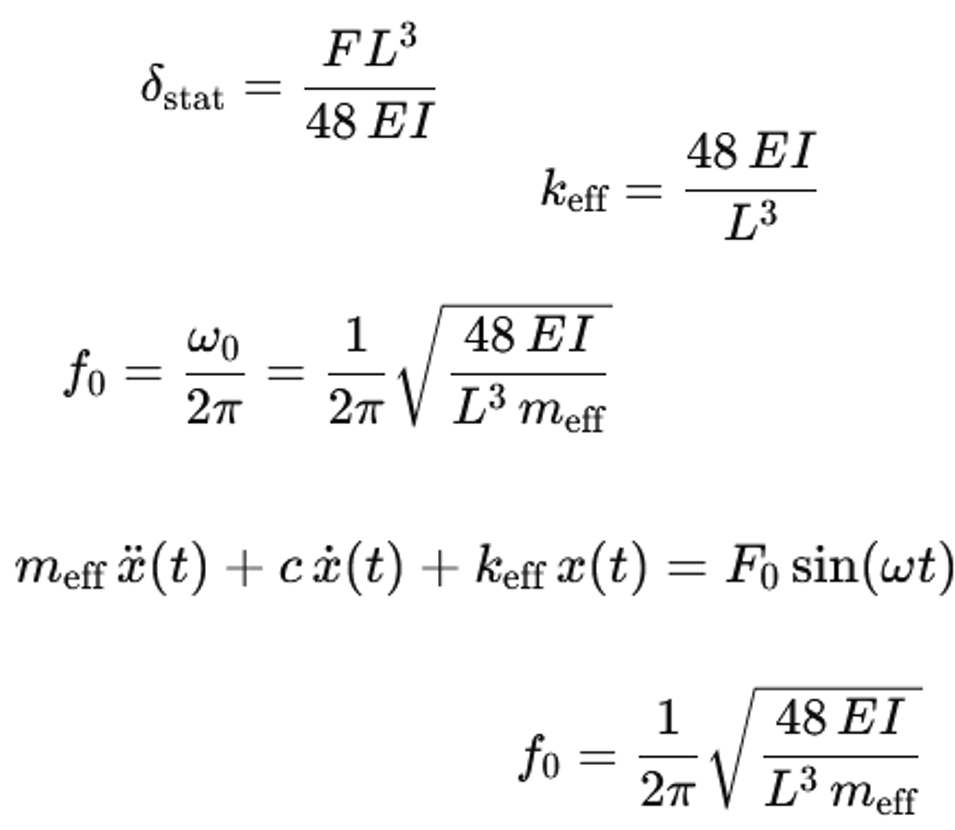
Corrección del desequilibrio en ejes giratorios

Ejemplo práctico: un eje giratorio horizontal se corrige a) estáticamente y b) dinámicamente mediante la adición o eliminación selectiva de masa en planos definidos, de modo que la fuerza de desequilibrio resultante o el momento de desequilibrio desaparecen o se reducen por debajo de un nivel de tolerancia. El equilibrado estático corrige un simple desplazamiento del centro de gravedad en un plano, mientras que el equilibrado dinámico corrige además las partes de desequilibrio basculantes mediante la compensación en dos (o más) planos a lo largo del eje.

1. Desbalance y frecuencia de excitación

Un eje giratorio con desequilibrio se describe mediante una masa excéntrica. Esta masa desequilibrada tiene una magnitud m_u y una distancia e desde el eje de rotación. El producto del desequilibrio es U=m_u e. El eje gira a una velocidad n en revoluciones por minuto. De ello se deriva la frecuencia de excitación en hercios f=n/60. La velocidad angular correspondiente es Ω=2πf=2πn/60.

La masa desequilibrada se mueve en una trayectoria circular y experimenta una fuerza centrífuga radial. El valor de esta fuerza es F_u=m_u eΩ^2=UΩ^2. Para la excitación de la vibración, nos interesa la proyección de esta fuerza en una dirección fija, por ejemplo, vertical. Esta proyección cambia armónicamente con el tiempo. Por lo tanto, la fuerza excitadora dependiente del tiempo se escribe como

F(t)=F_0 sin⁡(Ωt)

La amplitud F_0 es igual a m_u e〖 Ω〗^2.

2. Equilibrado estático

En el equilibrado estático se considera un eje esencialmente corto y macizo. El desequilibrio se puede modelar entonces como un desequilibrio puramente estático. Se coloca el eje de forma que gire con facilidad y se deja que oscile. El punto más pesado queda hacia abajo y marca la dirección del centro de gravedad. El objetivo es corregir el desequilibrio de manera que el centro de gravedad vuelva a situarse en el eje de rotación.

Si se coloca un contrapeso m_K en un radio r_K, su producto de desequilibrio debe compensar el original. Se aplica lo siguiente

m_K r_K=m_u e

En la práctica, se puede retirar material de la zona pesada o colocar un peso en el lado opuesto. Tras una corrección satisfactoria, el eje se mantiene en cualquier posición angular y ya no presenta oscilaciones.

3. Equilibrado dinámico

En el equilibrado dinámico se tiene en cuenta además el desequilibrio de momento. Para ello se utilizan dos planos de corrección a lo largo del eje. En cada plano se puede colocar un contrapeso con una masa y una posición angular determinadas. El eje gira a baja velocidad en una máquina equilibradora o en estado montado. Se miden las vibraciones y las posiciones de fase en los cojinetes.

Los vectores de vibración medidos se varían con pesos de prueba en ambos planos. A partir de los cambios se obtiene un sistema de ecuaciones lineales que describe la influencia de las masas de corrección. Este sistema proporciona las masas de corrección óptimas m_K1 y m_K2, así como sus posiciones angulares. Tras colocar los pesos de corrección, tanto el desequilibrio de fuerza como el desequilibrio de momento se reducen considerablemente y el eje funciona con mayor suavidad a la velocidad de funcionamiento.

4. Rigidez elástica del soporte

Para el cálculo de las vibraciones, el eje se describe a menudo mediante un sistema sustitutivo con una masa y un muelle. La rigidez vertical de una viga con un solo apoyo, con una luz L y una rigidez a la flexión EI, se determina a partir de la flexión estática. Se considera una carga puntual F en el centro de la viga. La flexión en el centro es

δ=(FL^3)/48EI

La rigidez efectiva del muelle en el centro se calcula como k=F/δ. De este modo se obtiene

k=48EI/L^3 

5. Masa efectiva y frecuencia natural

La masa oscilante se compone de la masa de la máquina y una parte de la masa de la viga. Se define una masa efectiva m_eff. Esta es aproximadamente m_eff=m_M+ηm_B. Aquí, m_M es la masa de la máquina y m_B es la masa del soporte. El factor de participación η suele estar en un rango de entre 0,2 y 0,3 aproximadamente. Si la máquina es mucho más pesada que el soporte, se establece aproximadamente m_eff≈m_M.

El sistema formado por la rigidez del muelle k y la masa m_eff constituye un oscilador de masa única. La ecuación del movimiento sin amortiguación es la siguiente:

m_eff  x ¨(t)+kx(t)=0

De esta ecuación se deduce la frecuencia natural

ω_0=√(k/m_eff )

La frecuencia propia en hercios es

f_0=ω_0/2π

Si se introduce k=48EI/L^3 para la viga, se obtiene

f_0=1/2π √(48EI/(L^3 m_eff ))

Esta relación muestra que la frecuencia natural aumenta con la rigidez a la flexión y disminuye con el aumento de la luz y la masa.

6. Consideración de la resonancia

Para comparar el riesgo de resonancia, se compara la frecuencia de excitación del desequilibrio con la frecuencia natural. La frecuencia de excitación es f=n/60. La frecuencia natural es f_0. Si ambas magnitudes son similares, es probable que se produzca resonancia. Si f es claramente inferior o superior a f_0, el riesgo de resonancia es menor. En la práctica, se prevé una distancia de seguridad para que el rango de resonancia no se encuentre en funcionamiento continuo.