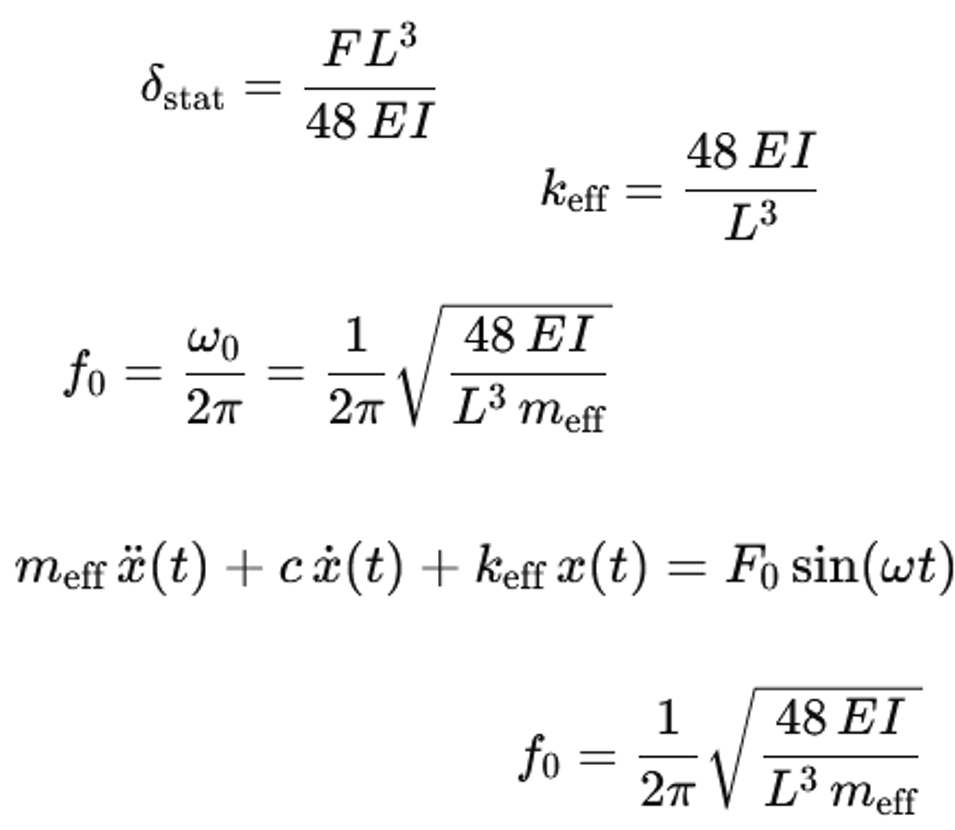
Correction du déséquilibre des arbres rotatifs

Exemple concret : un arbre tournant horizontalement est corrigé a) statiquement et b) dynamiquement par l'ajout ou le retrait ciblé de masse dans des plans définis, de manière à ce que la force de déséquilibre ou le moment de déséquilibre résultant disparaisse ou passe en dessous d'une tolérance. L'équilibrage statique corrige un simple déplacement du centre de gravité dans un plan, tandis que l'équilibrage dynamique corrige en plus les composantes de déséquilibre basculantes en compensant dans deux (ou plusieurs) plans le long de l'arbre.

1. Déséquilibre et fréquence d'excitation

Un arbre rotatif avec un déséquilibre est décrit par une masse excentrique. Cette masse déséquilibrée a une valeur m_u et une distance e par rapport à l'axe de rotation. Le produit du déséquilibre est U=m_u e. L'arbre tourne à la vitesse n en tours par minute. Il en résulte une fréquence d'excitation en hertz de f=n/60. La vitesse angulaire correspondante est Ω=2πf=2πn/60.

La masse d'équilibrage se déplace sur une trajectoire circulaire et subit une force centrifuge radiale. La valeur de cette force est F_u=m_u eΩ^2=UΩ^2. Pour l'excitation des vibrations, c'est la projection de cette force dans une direction fixe, par exemple verticale, qui nous intéresse. Cette projection varie harmoniquement avec le temps. On écrit donc la force d'excitation dépendante du temps comme suit

F(t)=F_0 sin⁡(Ωt)

L'amplitude F_0 est égale à m_u e〖 Ω〗^2.

2. Équilibrage statique

Lors de l'équilibrage statique, on considère un arbre essentiellement court et massif. Le déséquilibre peut alors être modélisé comme un déséquilibre purement statique. On monte l'arbre de manière très souple et on le laisse osciller. Le point le plus lourd se trouve en bas et marque la direction du centre de gravité. L'objectif est de corriger le déséquilibre de manière à ce que le centre de gravité se trouve à nouveau sur l'axe de rotation.

Si l'on ajoute un poids correcteur m_K dans un rayon r_K, son produit de déséquilibre doit compenser celui d'origine. On a alors

m_K r_K=m_u e

Concrètement, on peut soit retirer de la matière dans la zone lourde, soit ajouter un poids à l'opposé. Une fois la correction effectuée, l'arbre reste stable dans toutes les positions angulaires et ne présente plus aucun balancement.

3. Équilibrage dynamique

Lors de l'équilibrage dynamique, on tient également compte du déséquilibre de moment. Pour cela, deux plans de correction sont utilisés le long de l'arbre. Dans chaque plan, il est possible de fixer un poids de correction d'une masse et d'une position angulaire déterminées. L'arbre tourne à faible vitesse sur une machine d'équilibrage ou à l'état monté. Les vibrations et les positions de phase sont mesurées au niveau des paliers.

Les vecteurs d'oscillation mesurés sont modifiés à l'aide de poids d'essai dans les deux plans. Les modifications donnent lieu à un système d'équations linéaires qui décrit l'influence des masses de correction. Ce système fournit les masses de correction optimales m_K1 et m_K2 ainsi que leurs positions angulaires. Après la mise en place des poids de correction, le déséquilibre de force et le déséquilibre de couple sont fortement réduits et l'arbre tourne plus régulièrement à la vitesse de fonctionnement.

4. Rigidité élastique du support

Pour le calcul des vibrations, l'arbre est souvent décrit par un système équivalent avec une masse et un ressort. La rigidité verticale d'une poutre à simple appui avec une portée L et une rigidité à la flexion EI est déterminée par la flexion statique. On considère une charge ponctuelle F au milieu de la poutre. La flexion au milieu est

δ=(FL^3)/48EI

La rigidité effective du ressort au centre est donnée par k=F/δ. On obtient ainsi

k=48EI/L^3 

5. Masse effective et fréquence propre

La masse oscillante se compose de la masse de la machine et d'une partie de la masse de la poutre. On définit une masse effective m_eff. Celle-ci est approximativement égale à m_eff=m_M+ηm_B. Ici, m_M est la masse de la machine et m_B la masse du support. Le facteur de participation η se situe généralement dans une plage comprise entre 0,2 et 0,3 environ. Si la machine est beaucoup plus lourde que le support, on utilise approximativement m_eff≈m_M.

Le système composé de la rigidité du ressort k et de la masse m_eff forme un oscillateur à masse unique. L'équation du mouvement sans amortissement est la suivante

m_eff  x ¨(t)+kx(t)=0

Cette équation permet de calculer la fréquence propre

ω_0=√(k/m_eff )

La fréquence propre en hertz est de

f_0=ω_0/2π

Si l'on utilise k=48EI/L^3 pour la poutre, on obtient

f_0=1/2π √(48EI/(L^3 m_eff ))

Cette relation montre que la fréquence propre augmente avec la rigidité à la flexion et diminue avec l'augmentation de la portée et de la masse.

6. Analyse de la résonance

Pour évaluer le risque de résonance, on compare la fréquence d'excitation du déséquilibre avec la fréquence propre. La fréquence d'excitation est f=n/60. La fréquence propre est f_0. Si les deux valeurs sont proches l'une de l'autre, il faut s'attendre à une résonance. Si f est nettement inférieure ou supérieure à f_0, le risque de résonance est moindre. Dans la pratique, une marge de sécurité est prévue afin que la plage de résonance ne se trouve pas en fonctionnement continu.