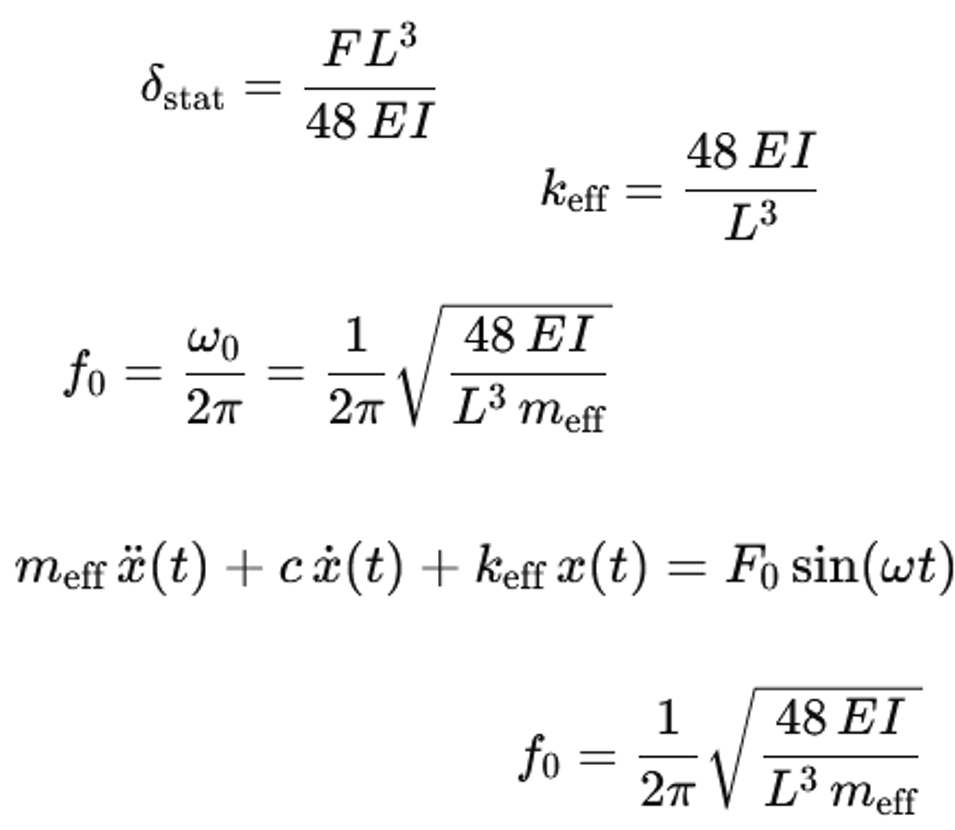
Correzione dello squilibrio negli alberi rotanti

Caso pratico: un albero rotante orizzontalmente viene corretto a) staticamente e b) dinamicamente mediante l'aggiunta o la rimozione mirata di massa in piani definiti, in modo tale che la forza di squilibrio risultante o il momento di squilibrio scompaiano o scendano al di sotto di una tolleranza. L'equilibratura statica corregge un puro spostamento del baricentro in un piano, mentre l'equilibratura dinamica corregge anche le componenti di squilibrio inclinate mediante compensazione in due (o più) piani lungo l'albero.

1. Squilibrio e frequenza di eccitazione

Un albero rotante con uno squilibrio è descritto da una massa eccentrica. Questa massa squilibrata ha dimensione m_u e distanza e dall'asse di rotazione. Il prodotto dello squilibrio è U=m_u e. L'albero ruota con una velocità n in giri al minuto. Ne risulta la frequenza di eccitazione in Hertz pari a f=n/60. La velocità angolare corrispondente è Ω=2πf=2πn/60.

La massa sbilanciata si muove su una traiettoria circolare e subisce una forza centrifuga radiale. Il valore di questa forza è F_u=m_u eΩ^2=UΩ^2. Per l'eccitazione delle vibrazioni è interessante la proiezione di questa forza in una direzione fissa, ad esempio verticale. Questa proiezione varia armonicamente nel tempo. Pertanto, la forza di eccitazione dipendente dal tempo viene scritta come

F(t)=F_0 sin⁡(Ωt)

L'ampiezza F_0 è pari a m_u e〖 Ω〗^2.

2. Bilanciamento statico

Nell'equilibratura statica si considera un albero essenzialmente corto e massiccio. Lo squilibrio può quindi essere modellato come uno squilibrio puramente statico. Si supporta l'albero in modo che scorra molto facilmente e lo si lascia oscillare. Il punto più pesante scende verso il basso e segna la direzione del baricentro. L'obiettivo è correggere lo squilibrio in modo che il baricentro torni sull'asse di rotazione.

Se si applica un peso correttivo m_K con un raggio r_K, il suo prodotto di squilibrio deve compensare quello originale. Vale quanto segue

m_K r_K=m_u e

In pratica è possibile rimuovere materiale dalla zona pesante oppure applicare un peso sul lato opposto. Una volta effettuata la correzione, l'albero rimane fermo in qualsiasi posizione angolare e non oscilla più.

3. Bilanciamento dinamico

Durante l'equilibratura dinamica si tiene conto anche dello squilibrio momentaneo. A tal fine vengono utilizzati due piani di correzione lungo l'albero. In ciascun piano è possibile applicare un contrappeso con una massa e una posizione angolare determinate. L'albero gira su una macchina equilibratrice o, una volta montato, a bassa velocità. Le vibrazioni e le posizioni di fase vengono misurate sui cuscinetti.

I vettori di vibrazione misurati vengono variati con pesi di prova nei due piani. Dalle variazioni risulta un sistema di equazioni lineari che descrive l'influenza delle masse di correzione. Questo sistema fornisce le masse di correzione ottimali m_K1 e m_K2 e le loro posizioni angolari. Dopo aver applicato i pesi di correzione, sia lo squilibrio di forza che lo squilibrio di momento sono notevolmente ridotti e l'albero gira in modo più regolare alla velocità di esercizio.

4. Rigidità elastica del supporto

Per il calcolo delle vibrazioni, l'albero viene spesso descritto da un sistema sostitutivo con una massa e una molla. La rigidità verticale di una trave a supporto singolo con campata L e rigidità alla flessione EI viene determinata tramite la flessione statica. Si considera un carico singolo F al centro della trave. La flessione al centro è

δ=(FL^3)/48EI

La rigidità effettiva della molla al centro è data da k=F/δ. Si ottiene quindi

k=48EI/L^3 

5. Massa effettiva e frequenza naturale

La massa oscillante è costituita dalla massa della macchina e da una parte della massa della trave. Si definisce una massa effettiva m_eff. Questa è approssimativamente m_eff=m_M+ηm_B. Qui m_M è la massa della macchina e m_B è la massa della trave. Il fattore di partecipazione η è tipicamente compreso in un intervallo compreso tra 0,2 e 0,3. Se la macchina è molto più pesante della trave, si imposta approssimativamente m_eff≈m_M.

Il sistema costituito dalla rigidità elastica k e dalla massa m_eff forma un oscillatore a massa singola. L'equazione del moto senza smorzamento è la seguente

m_eff  x ¨(t)+kx(t)=0

Da questa equazione deriva la frequenza propria

ω_0=√(k/m_eff )

La frequenza naturale in Hertz è pari a

f_0=ω_0/2π

Se si inserisce k=48EI/L^3 per la trave, si ottiene

f_0=1/2π √(48EI/(L^3 m_eff ))

Questa relazione mostra che la frequenza naturale aumenta con la rigidità alla flessione e diminuisce con l'aumentare della campata e della massa.

6. Considerazioni sulla risonanza

Per valutare il rischio di risonanza, si confronta la frequenza di eccitazione dello squilibrio con la frequenza naturale. La frequenza di eccitazione è f=n/60. La frequenza naturale è f_0. Se entrambe le grandezze sono vicine tra loro, è probabile che si verifichi risonanza. Se f è nettamente inferiore o superiore a f_0, il rischio di risonanza è minore. Nella pratica si prevede un margine di sicurezza affinché la zona di risonanza non si trovi in funzionamento continuo.