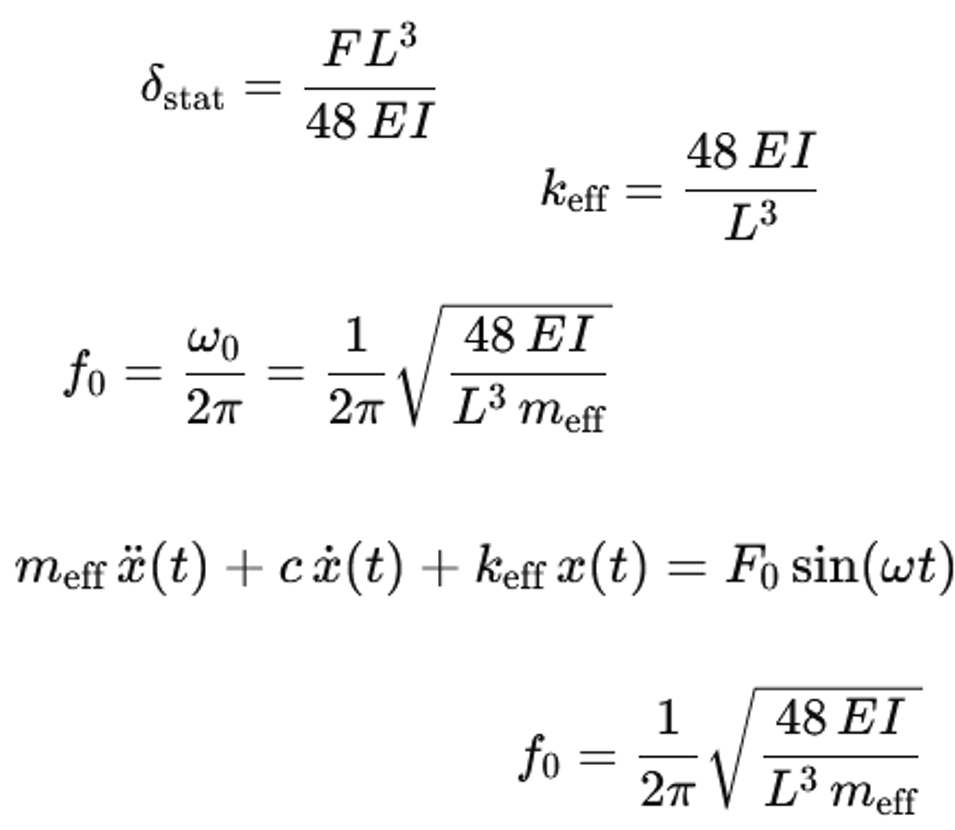
Коррекция дисбаланса вращающихся валов

Пример: горизонтально вращающийся вал корректируется а) статически и б) динамически путем целенаправленного добавления или удаления массы в определенных плоскостях таким образом, что результирующая сила дисбаланса или момент дисбаланса исчезают или снижаются до уровня, не превышающего допустимую погрешность. Статическая балансировка корректирует чистое смещение центра тяжести в одной плоскости, динамическая балансировка дополнительно корректирует наклонные компоненты дисбаланса путем выравнивания в двух (или более) плоскостях вдоль вала.

1. Несбалансированность и частота возбуждения

Вращающийся вал с дисбалансом описывается эксцентричной массой. Эта дисбалансная масса имеет величину m_u и расстояние e от оси вращения. Продукт дисбаланса равен U=m_u e. Вал вращается со скоростью n оборотов в минуту. Отсюда следует, что частота возбуждения в герцах равна f=n/60. Соответствующая угловая скорость равна Ω=2πf=2πn/60.

Неуравновешенная масса движется по круговой траектории и испытывает радиальную центробежную силу. Величина этой силы равна F_u=m_u eΩ^2=UΩ^2. Для возбуждения колебаний интерес представляет проекция этой силы в фиксированном направлении, например, по вертикали. Эта проекция изменяется гармонически со временем. Поэтому зависимость возбуждающей силы от времени записывается как

F(t)=F_0 sin⁡(Ωt)

Амплитуда F_0 равна m_u e〖 Ω〗^2.

2. Статическая балансировка

При статическом балансировании рассматривается в основном короткий массивный вал. Несбалансированность в этом случае можно смоделировать как чисто статическую. Вал устанавливается на подшипники с очень легким ходом и дается возможность раскачиваться. Самая тяжелая точка опускается вниз и обозначает направление центра тяжести. Цель состоит в том, чтобы скорректировать несбалансированность таким образом, чтобы центр тяжести снова находился на оси вращения.

Если установить корректирующий груз m_K на радиусе r_K, то его продукт дисбаланса должен компенсировать исходный. При этом выполняется следующее условие

m_K r_K=m_u e

На практике можно либо удалить материал в проблемной зоне, либо установить противовес на противоположной стороне. После успешной корректировки вал остается в любом угловом положении и больше не колеблется.

3. Динамическая балансировка

При динамической балансировке дополнительно учитывается моментный дисбаланс. Для этого используются две плоскости корректировки вдоль вала. В каждой плоскости можно установить корректирующий груз с определенной массой и угловым положением. Вал работает на балансировочном станке или в установленном состоянии с низкой скоростью вращения. На подшипниках измеряются колебания и фазовые положения.

Измеренные векторы колебаний варьируются с помощью тестовых грузов в обеих плоскостях. Из изменений получается линейная система уравнений, которая описывает влияние корректирующих масс. Эта система дает оптимальные корректирующие массы m_K1 и m_K2, а также их угловые положения. После установки корректирующих грузов как дисбаланс силы, так и дисбаланс момента значительно уменьшаются, и вал работает более плавно при рабочей скорости.

4. Жесткость пружины опоры

Для расчета колебаний вал часто описывается с помощью эквивалентной системы с массой и пружиной. Вертикальная жесткость просто подвешенной балки с пролетом L и жесткостью на изгиб EI определяется по статической прогибе. Рассматривается единичная нагрузка F в середине балки. Прогиб в середине составляет

δ=(FL^3)/48EI

Эффективная жесткость пружины в центре равна k=F/δ. Таким образом, получаем

k=48EI/L^3 

5. Эффективная масса и собственная частота

Колеблющаяся масса состоит из массы машины и части массы балки. Определяется эффективная масса m_eff. Она приблизительно равна m_eff=m_M+ηm_B. Здесь m_M — масса машины, а m_B — масса опоры. Коэффициент участия η обычно находится в диапазоне от 0,2 до 0,3. Если машина значительно тяжелее опоры, то приблизительно m_eff≈m_M.

Система, состоящая из жесткости пружины k и массы m_eff, образует одномассовый колебательный механизм. Уравнение движения без демпфирования имеет вид

m_eff  x ¨(t)+kx(t)=0

Из этого уравнения следует собственная частота колебаний

ω_0=√(k/m_eff )

Собственная частота в герцах составляет

f_0=ω_0/2π

Если для балки использовать k=48EI/L^3, то получается

f_0=1/2π √(48EI/(L^3 m_eff ))

Эта зависимость показывает, что собственная частота увеличивается с ростом жесткости на изгиб и уменьшается с ростом размаха и массы.

6. Анализ резонанса

Для оценки риска резонанса сравнивают частоту возбуждения дисбаланса с собственной частотой. Частота возбуждения равна f=n/60. Собственная частота равна f_0. Если обе величины близки друг к другу, следует ожидать резонанса. Если f значительно ниже или значительно выше f_0, риск резонанса меньше. На практике предусматривается запас прочности, чтобы область резонанса не находилась в режиме непрерывной работы.