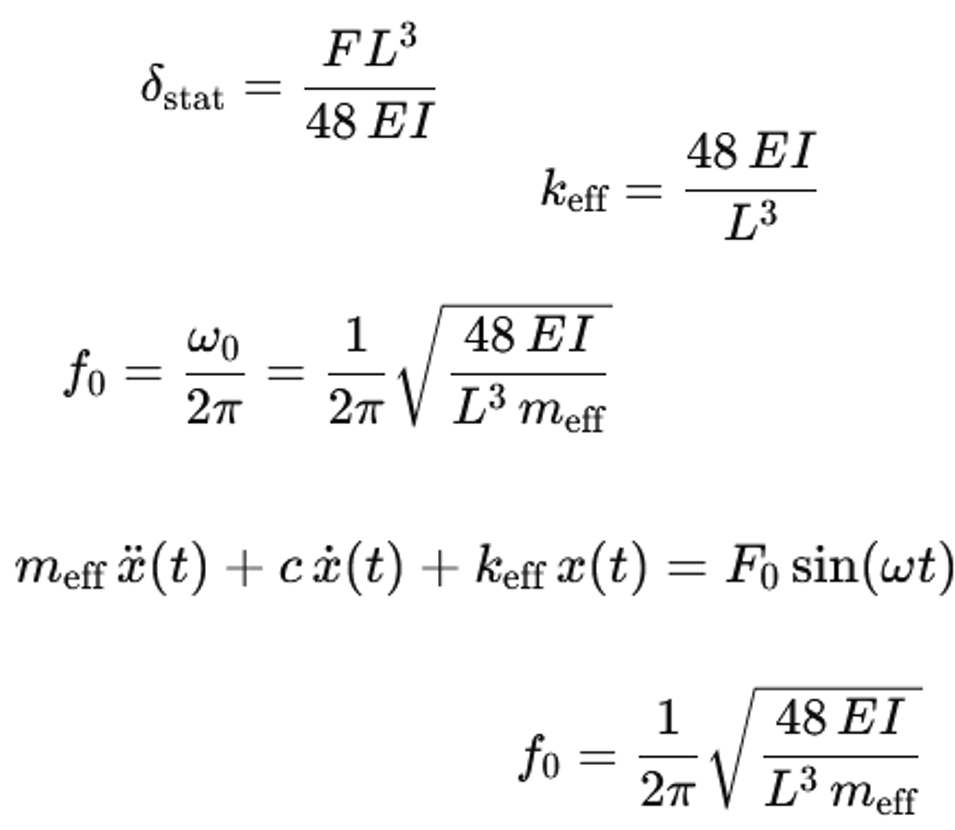
Korygowanie niewyważenia wałów obrotowych

Przykład: Wał obracający się w poziomie jest korygowany a) statycznie i b) dynamicznie poprzez celowe dodawanie lub usuwanie masy w określonych płaszczyznach w taki sposób, aby wynikowa siła niewyważenia lub moment niewyważenia zniknęły lub spadły poniżej tolerancji. Wyważanie statyczne koryguje czyste przesunięcie środka ciężkości w jednej płaszczyźnie, natomiast wyważanie dynamiczne dodatkowo koryguje przechylające się elementy niewyważenia poprzez wyrównanie w dwóch (lub więcej) płaszczyznach wzdłuż wału.

1. Wyważenie i częstotliwość wzbudzenia

Wał obrotowy z niewyważeniem jest opisywany przez masę mimośrodową. Ta masa niewyważenia ma wielkość m_u i odległość e od osi obrotu. Wynikiem niewyważenia jest U=m_u e. Wał obraca się z prędkością n obrotów na minutę. Wynika z tego częstotliwość wzbudzenia w hercach f=n/60. Odpowiednia prędkość kątowa wynosi Ω=2πf=2πn/60.

Masa niewyważona porusza się po torze kołowym i podlega promieniowej sile odśrodkowej. Wielkość tej siły wynosi F_u=m_u eΩ^2=UΩ^2. Dla wzbudzenia drgań interesuje nas rzut tej siły w stałym kierunku, na przykład w pionie. Rzut ten zmienia się harmonicznie w czasie. Dlatego też siłę wzbudzającą zależną od czasu zapisuje się jako

F(t)=F_0 sin⁡(Ωt)

Amplituda F_0 jest równa m_u e〖 Ω〗^2.

2. Wyważanie statyczne

W przypadku wyważania statycznego bierze się pod uwagę zasadniczo krótki, masywny wał. Wyważenie można wówczas modelować jako czyste wyważenie statyczne. Wał umieszcza się na bardzo płynnym łożysku i pozwala mu się wyważyć. Najcięższe miejsce opada w dół i wyznacza kierunek środka ciężkości. Celem jest skorygowanie wyważenia w taki sposób, aby środek ciężkości ponownie znalazł się na osi obrotu.

Jeśli zamontuje się ciężarek korekcyjny m_K w promieniu r_K, to jego produkt niewyważenia musi zrównoważyć pierwotny. Obowiązuje następująca zasada

m_K r_K=m_u e

W praktyce można albo usunąć materiał w trudnym obszarze, albo zamontować obciążnik po przeciwnej stronie. Po pomyślnej korekcie wał pozostaje w dowolnym położeniu kątowym i nie wykazuje już żadnych drgań.

3. Wyważanie dynamiczne

Podczas wyważania dynamicznego uwzględnia się dodatkowo niewyważenie momentowe. W tym celu stosuje się dwie płaszczyzny korekcyjne wzdłuż wału. Na każdej płaszczyźnie można zamontować obciążnik korekcyjny o określonej masie i położeniu kątowym. Wał obraca się na wyważarce lub w stanie zamontowanym z niską prędkością obrotową. Na łożyskach mierzy się drgania i położenia fazowe.

Zmierzone wektory drgań są zmieniane za pomocą obciążników testowych w obu płaszczyznach. Zmiany te dają liniowy układ równań, który opisuje wpływ mas korekcyjnych. Układ ten dostarcza optymalne masy korekcyjne m_K1 i m_K2 oraz ich pozycje kątowe. Po zamontowaniu ciężarków korekcyjnych zarówno niewyważenie siły, jak i niewyważenie momentu obrotowego ulegają znacznemu zmniejszeniu, a wał pracuje płynniej przy prędkości roboczej.

4. Sztywność sprężyny wspornika

W celu obliczenia drgań wał jest często opisywany za pomocą układu zastępczego z masą i sprężyną. Sztywność pionowa belki o rozpiętości L i sztywności zginania EI jest określana na podstawie statycznego ugięcia. Rozpatruje się pojedyncze obciążenie F w środku belki. Ugięcie w środku wynosi

δ=(FL^3)/48EI

Efektywna sztywność sprężyny w środku wynosi k=F/δ. W ten sposób otrzymujemy

k=48EI/L^3 

5. Masa efektywna i częstotliwość drgań własnych

Masa drgająca składa się z masy maszyny i części masy belki. Definiuje się masę efektywną m_eff. Jest ona w przybliżeniu równa m_eff=m_M+ηm_B. Tutaj m_M jest masą maszyny, a m_B masą belki. Współczynnik udziału η wynosi zazwyczaj od około 0,2 do 0,3. Jeśli maszyna jest znacznie cięższa od belki, przyjmuje się w przybliżeniu m_eff≈m_M.

System składający się ze sztywności sprężyny k i masy m_eff tworzy oscylator jednokomponentowy. Równanie ruchu bez tłumienia brzmi następująco

m_eff  x ¨(t)+kx(t)=0

Z tego równania wynika częstotliwość własna

ω_0=√(k/m_eff )

Częstotliwość własna w hercach wynosi

f_0=ω_0/2π

Jeśli dla belki zastosujemy k=48EI/L^3, otrzymamy wynik

f_0=1/2π √(48EI/(L^3 m_eff ))

Zależność ta pokazuje, że częstotliwość własna wzrasta wraz ze sztywnością na zginanie, a maleje wraz ze wzrostem rozpiętości i masy.

6. Analiza rezonansu

Aby wyeliminować ryzyko rezonansu, porównuje się częstotliwość wzbudzającą niewyważenie z częstotliwością własną. Częstotliwość wzbudzająca wynosi f=n/60. Częstotliwość własna wynosi f_0. Jeśli obie wartości są zbliżone, należy spodziewać się rezonansu. Jeśli f jest znacznie niższe lub znacznie wyższe od f_0, ryzyko rezonansu jest mniejsze. W praktyce przewiduje się bezpieczny odstęp, aby zakres rezonansu nie znajdował się w trybie ciągłej pracy.