Oberflächenvergrößerung
Oberflächenvergrößerung bezeichnet im Kontext von Schüttgütern und Pulvern die Zerkleinerung von Feststoffen. Durch die Zerkleinerung wird ein grober Feststoff in eine große Anzahl kleinerer Partikel überführt. Mit abnehmender Partikelgröße steigt die spezifische Oberfläche, also die frei zugängliche Oberfläche bezogen auf die Masse des Feststoffs.
Die Zerkleinerung kann trocken oder nass erfolgen. Bei der Trockenmahlung wird ohne flüssiges Medium gearbeitet. Bei der Nassmahlung sind die Partikel in einer Flüssigkeit suspendiert. Die Wahl des Zerkleinerungsverfahrens hängt vom Werkstoff, von der angestrebten Feinheit sowie von prozesstechnischen Randbedingungen ab.
Für die Zerkleinerung von Feststoffen stehen zahlreiche Maschinentypen zur Verfügung. Dazu zählen Klumpenbrecher, Prallbackenzerkleinerer, Walzenmühlen, Reibzerkleinerer, Hammermühlen, Luftstrahlmühlen, Kollergänge, Kugelmühlen, Rührwerkskugelmühlen, Schwingmühlen, Stiftmühlen, Schneidmühlen, Scheibenmühlen, Planetenkugelmühlen, Desagglomeratoren und Sichtermühlen. Die Verfahren unterscheiden sich in der Art der Krafteinwirkung, etwa durch Druck, Schlag, Prall, Scherung oder Reibung.
Eine besondere Form der Feststoffzerkleinerung ist das Kondensieren. Dabei werden Dämpfe oder Aerosole aus Metallschmelzen rasch abgekühlt, sodass feste Nanopartikel entstehen. Auch das Versprühen von Metallschmelzen, beispielsweise durch Gasverdüsung, stellt eine Methode der Oberflächenvergrößerung dar. Solche Verfahren werden zur Herstellung metallischer Pulver mit definierter Partikelgröße eingesetzt. Eine weitere Methode ist die Pyrolyse, mit deren Hilfe nanostrukturierte Schwarzpigmente hergestellt werden.
Die Geometrie der entstehenden Partikel hängt sowohl vom Ausgangsstoff als auch vom Zerkleinerungsmechanismus ab. Partikel können annähernd kugelförmig sein. Sie können unregelmäßig, kantig, scharf oder splitterartig auftreten. Kristalline Feststoffe zeigen häufig facettierte, kristallähnliche Formen. Diese Eigenschaften beeinflussen das Fließverhalten, die Schüttdichte, die Mischbarkeit und die Reaktivität eines Pulvers.
Die Oberflächenvergrößerung führt dazu, dass ein Feststoff mit abnehmender Partikelgröße wirksamer wird. Dies lässt sich besonders anschaulich an Farbpigmenten zeigen. Sehr kleine Mengen fein zerkleinerter Pigmente reichen aus, um große Mengen von Pulvern, Kunststoffen oder Textilien intensiv einzufärben. Die Farbwirkung hängt unmittelbar von der frei zugänglichen Oberfläche der Pigmentpartikel ab.
Mit zunehmender Feinheit steigen die Adhäsionskräfte zwischen den Partikeln. Sehr feine Pulver neigen daher stark zur Agglomeration. Nanofeines, trockenes Keramikpulver aus der Hochleistungs- und Ingenieurkeramik kann sich ähnlich klebrig verhalten wie ein gröberes Pulver, das zuvor befeuchtet wurde. Sobald sich solche Partikel relativ zueinander bewegen, bilden sich Agglomerate. Bestehen diese aus nanofeinen Primärpartikeln, können sie eine sehr hohe mechanische Festigkeit aufweisen.
Solche Agglomerate lassen sich in Hochleistungsmischern aus dem Hause amixon® wirksam desagglomerieren, insbesondere dann, wenn Nanopulver gleichzeitig mit weiteren Pulverkomponenten homogen vermischt werden sollen. Alternativ ist auch eine Desagglomeration in Mahlanlagen möglich, beispielsweise in Luftstrahlmühlen.
Der Zusammenhang zwischen Zerkleinerung und Oberflächenvergrößerung lässt sich geometrisch veranschaulichen. Ausgangspunkt ist ein regelmäßig geformter Quader mit der Kantenlänge L. Sein Volumen beträgt L³, seine Oberfläche 6·L². Wird der Quader in einem Zerkleinerungsschritt in allen drei Raumrichtungen halbiert, entstehen acht gleich große Quader mit der Kantenlänge L/2.
Nach n Zerkleinerungsschritten ergibt sich die Anzahl der Partikel zu
N(n) = 8ⁿ
Die Oberfläche eines einzelnen Partikels beträgt
A₁(n) = 6·(L/2ⁿ)²
Die gesamte Oberfläche aller Partikel ergibt sich zu
A₍ges₎(n) = N(n) · A₁(n) = 6·L²·2ⁿ
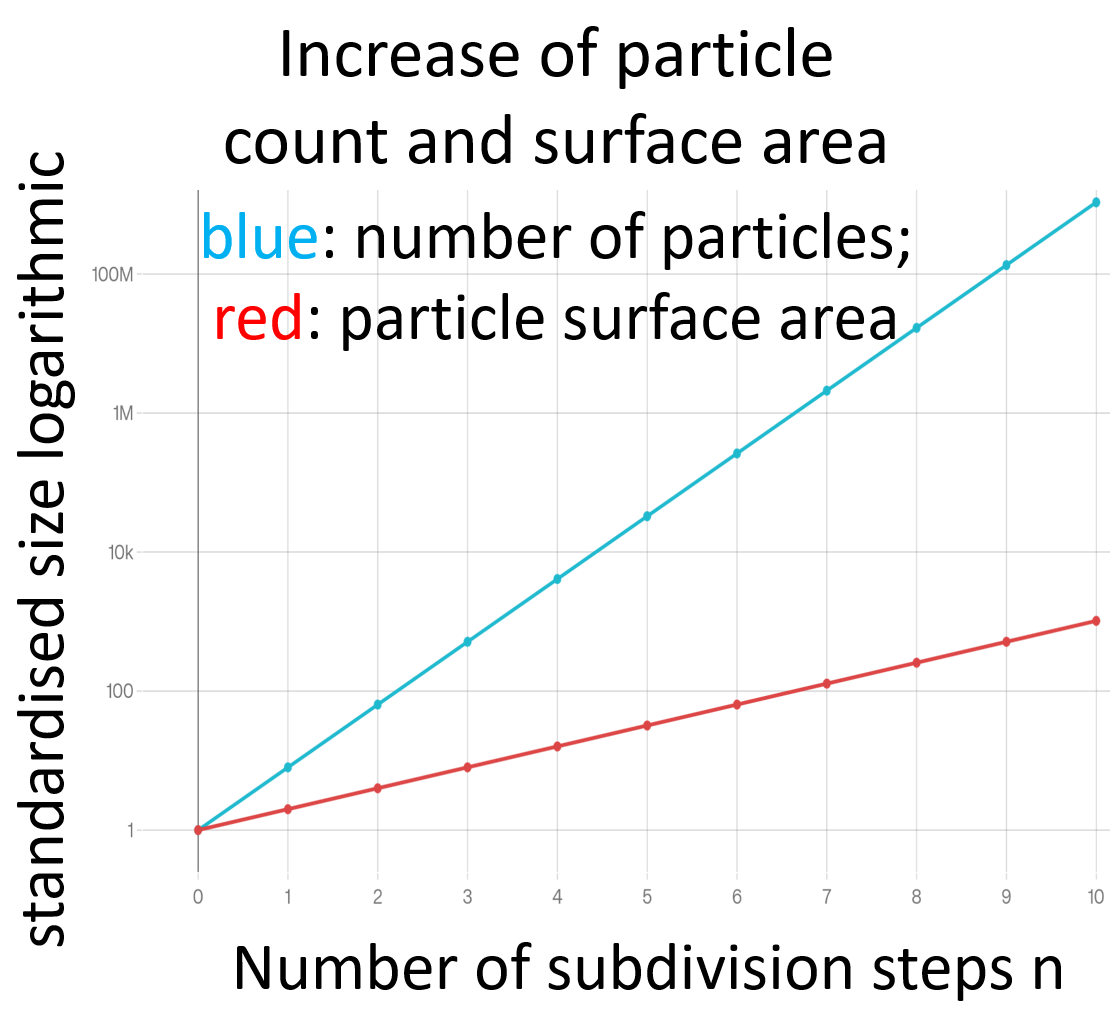
Die Anzahl der Partikel wächst damit exponentiell mit der Anzahl der Zerkleinerungsschritte. Auch die Gesamtoberfläche nimmt exponentiell zu, jedoch mit geringerer Steigung. Für grafische Darstellungen ist daher eine logarithmische Skalierung der Ordinate sinnvoll.
Diese geometrischen und energetischen Betrachtungen verdeutlichen, wie stark Zerkleinerungsvorgänge die physikalischen und chemischen Eigenschaften von Pulvern verändern. Medizinische Wirkstoffe können besser mit biologischen Systemen interagieren. Neue Hochleistungswerkstoffe entstehen durch das Sintern feinster Pulver, etwa für Anwendungen in der Elektrochemie, der Hochtemperaturtechnik, der Supraleitung, der Optoelektronik, der Sensorik, der Nachrichtentechnik oder der Energiegewinnung.
Der für die Zerkleinerung erforderliche Energieaufwand E ist hoch. Er hängt vom Zerkleinerungsgrad ab. Zur Beschreibung dieses Zusammenhangs haben sich in der Zerkleinerungstechnik drei klassische Energiegesetze etabliert.
Das Rittinger-Gesetz geht davon aus, dass der Energiebedarf proportional zur neu gebildeten Oberfläche ist. Es eignet sich besonders für die Fein- und Feinstmahlung. Der spezifische Energieaufwand ergibt sich zu
Eₛ = KR · (1/d₂ − 1/d₁)
- d1: charakteristische Ausgangskorngröße, d2d_2d2: Endkorngröße (z. B. d80 oder d50)
- KR: Werkstoff-/Prozesskonstante
Das Kick-Gesetz beschreibt den Energieaufwand als Funktion des Zerkleinerungsverhältnisses. Es ist vor allem für die Grobzerkleinerung geeignet. Es wird geometrische Ähnlichkeit der Partikel angenommen. Der spezifische Energieaufwand lautet
Eₛ = KK · ln (d₁/d₂)
Das Bond-Gesetz wir für mittlere Mahlgrade verwendet. Es stellt einen praxisnahen Kompromiss zwischen beiden Ansätzen dar und wird häufig im mittleren Zerkleinerungsbereich angewendet. Es berücksichtigt, dass der Energiebedarf mit der Quadratwurzel der Korngröße zusammenhängt. Der spezifische Energieaufwand ergibt sich zu
Eₛ = KB · (1/√d₂ − 1/√d₁)
- d1 ist die charakteristische Korngröße des Aufgabematerials
- d2 ist die charakteristische Korngröße des Mahlprodukts
In der industriellen Praxis wird das Bond-Gesetz häufig in Form des Bond Work Index verwendet. Dabei werden charakteristische Korngrößen wie der 80-%-Durchgang der Aufgabe F₈₀ und des Produkts P₈₀ eingesetzt. Die gebräuchliche Bond-Gleichung lautet
Es = 10 · Wi · (1 / √P80 − 1 / √F80)
- F80: Korngröße, bei der 80 % der Aufgabe feiner sind
- P80: Korngröße, bei der 80 % des Produkts feiner sind
- Es in kWh/t
- Wi = Bond Work Index (materialspezifische Konstante)
- F80, P80 in µm
Nanofeine Pulver können jedoch auch unerwünschte Wirkungen entfalten. Reifenabrieb oder Mikro-Kunststoffpartikel können zu einer Belastung von Atemluft und Trinkwasser führen. Körpereigene Schutzmechanismen können sich gegen Fremdstoffe nur eingeschränkt wehren, wenn diese nanopartikulär oder nanostrukturiert vorliegen.

