Zwiększenie powierzchni
W kontekście materiałów sypkich i proszków zwiększenie powierzchni oznacza rozdrobnienie substancji stałych. W wyniku rozdrobnienia gruboziarnista substancja stała zostaje przekształcona w dużą liczbę mniejszych cząstek. Wraz ze zmniejszaniem się wielkości cząstek wzrasta powierzchnia właściwa, czyli powierzchnia swobodnie dostępna w stosunku do masy substancji stałej.
Rozdrabnianie może odbywać się na sucho lub na mokro. W przypadku mielenia na sucho nie stosuje się medium płynnego. W przypadku mielenia na mokro cząstki są zawieszone w cieczy. Wybór metody rozdrabniania zależy od materiału, pożądanej drobności oraz warunków brzegowych procesu.
Do rozdrabniania substancji stałych dostępnych jest wiele rodzajów maszyn. Należą do nich kruszarki do brył, kruszarki udarowe, młyny walcowe, kruszarki tarciowe, młyny młotkowe, młyny strumieniowe, młyny walcowe, młyny kulowe, młyny kulowe z mieszadłem, młyny wibracyjne, młyny szpilkowe, młyny tnące, młyny tarczowe, młyny kulowe planetarne, dezagregatory i młyny sortujące. Procesy te różnią się rodzajem oddziaływania siły, np. poprzez nacisk, uderzenie, zderzenie, ścinanie lub tarcie.
Szczególną formą rozdrabniania ciał stałych jest kondensacja. Polega ona na szybkim schładzaniu oparów lub aerozoli ze stopionych metali, co powoduje powstawanie stałych nanocząstek. Rozpylanie stopionych metali, na przykład poprzez atomizację gazową, jest również metodą zwiększania powierzchni. Procesy takie są stosowane do produkcji proszków metalicznych o określonej wielkości cząstek. Inną metodą jest piroliza, za pomocą której wytwarza się nanostrukturalne czarne pigmenty.
Geometria powstających cząstek zależy zarówno od materiału wyjściowego, jak i od mechanizmu rozdrabniania. Cząstki mogą mieć kształt zbliżony do kulistego. Mogą być nieregularne, kanciaste, ostre lub w kształcie odłamków. Ciała stałe krystaliczne często mają fasetowane, kryształopodobne kształty. Właściwości te wpływają na właściwości płynięcia, gęstość nasypową, mieszalność i reaktywność proszku.
Zwiększenie powierzchni powoduje, że ciało stałe staje się bardziej skuteczne wraz ze zmniejszaniem się wielkości cząstek. Można to szczególnie dobrze zaobserwować na przykładzie pigmentów barwiących. Bardzo małe ilości drobno rozdrobnionych pigmentów wystarczają do intensywnego zabarwienia dużych ilości proszków, tworzyw sztucznych lub tekstyliów. Efekt barwny zależy bezpośrednio od swobodnie dostępnej powierzchni cząstek pigmentu.
Wraz ze wzrostem drobności wzrastają siły adhezji między cząstkami. Bardzo drobne proszki mają zatem silną tendencję do aglomeracji. Nanodrobny, suchy proszek ceramiczny z ceramiki wysokowydajnej i inżynieryjnej może zachowywać się podobnie jak grubszy proszek, który został wcześniej zwilżony. Gdy tylko takie cząstki poruszają się względem siebie, tworzą się aglomeraty. Jeśli składają się one z nanodrobnych cząstek pierwotnych, mogą wykazywać bardzo wysoką wytrzymałość mechaniczną.
Takie aglomeraty można skutecznie dezagregować w wysokowydajnych mieszalnikach firmy amixon®, zwłaszcza gdy nanoproszek ma być jednocześnie mieszany z innymi składnikami proszkowymi w sposób homogeniczny. Alternatywnie możliwa jest również dezagregacja w urządzeniach do mielenia, na przykład w młynach strumieniowych.
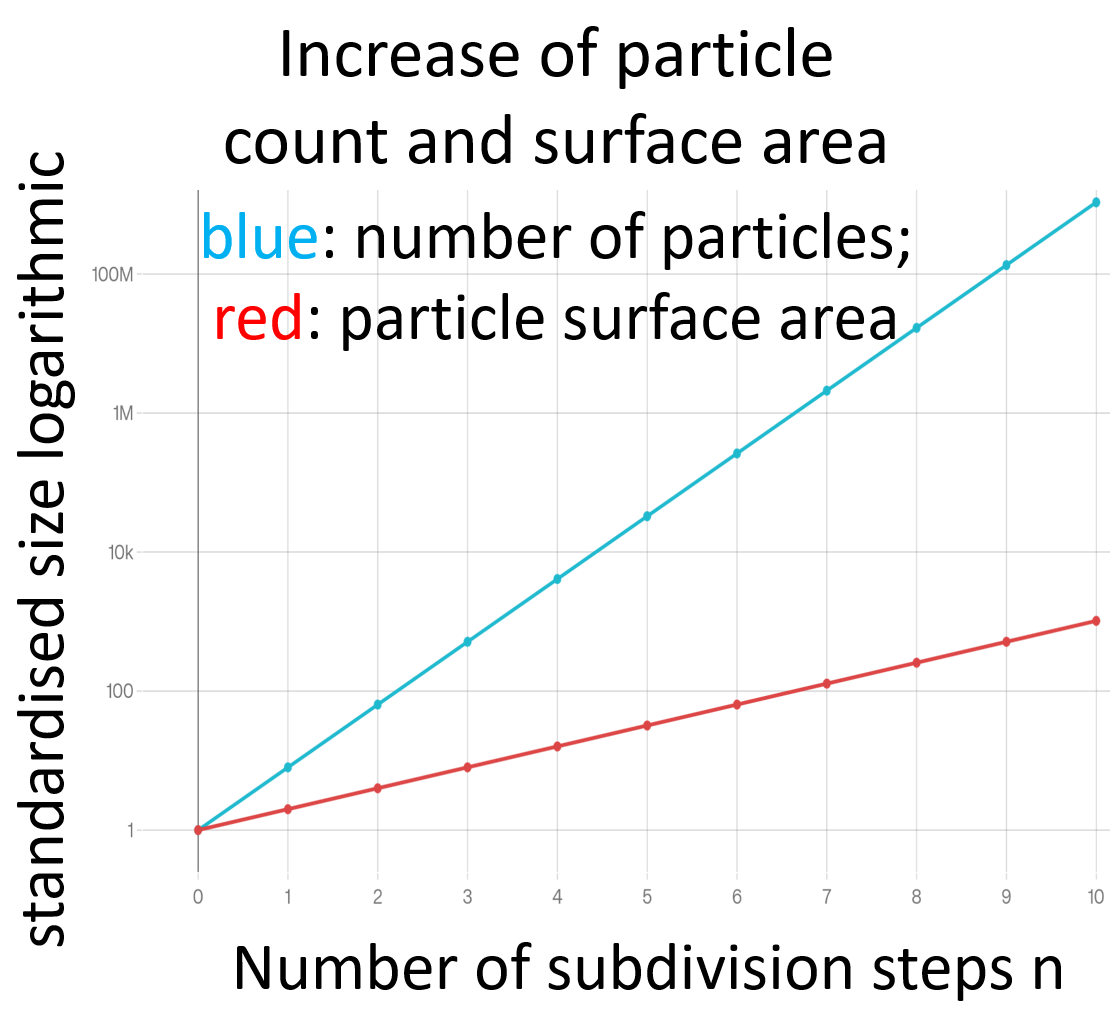
Związek między rozdrabnianiem a zwiększeniem powierzchni można zilustrować geometrycznie. Punktem wyjścia jest prostopadłościan o regularnym kształcie i długości krawędzi L. Jego objętość wynosi L³, a powierzchnia 6·L². Jeśli prostopadłościan zostanie podzielony na pół we wszystkich trzech kierunkach przestrzennych w jednym etapie rozdrabniania, powstaje osiem prostopadłościanów o tej samej wielkości i długości krawędzi L/2.
Po n etapach rozdrabniania liczba cząstek wynosi
N(n) = 8ⁿ
Powierzchnia pojedynczej cząstki wynosi
A₁(n) = 6·(L/2ⁿ)²
Całkowita powierzchnia wszystkich cząstek wynosi
A₍ges₎(n) = N(n) · A₁(n) = 6·L²·2ⁿ
Liczba cząstek rośnie zatem wykładniczo wraz z liczbą etapów rozdrabniania. Całkowita powierzchnia również rośnie wykładniczo, ale z mniejszym nachyleniem. W przypadku przedstawień graficznych sensowne jest zatem zastosowanie skali logarytmicznej na osi rzędnych.
Te rozważania geometryczne i energetyczne pokazują, jak silnie procesy rozdrabniania zmieniają właściwości fizyczne i chemiczne proszków. Substancje czynne leków mogą lepiej oddziaływać z układami biologicznymi. Nowe materiały o wysokiej wydajności powstają w wyniku spiekania najdrobniejszych proszków, na przykład do zastosowań w elektrochemii, technologii wysokotemperaturowej, nadprzewodnictwie, optoelektronice, czujnikach, technologii komunikacyjnej lub wytwarzaniu energii.
Zużycie energii wymagane do rozdrabniania E jest wysokie. Zależy ono od stopnia rozdrobnienia. Aby opisać tę zależność, w technice rozdrabniania przyjęto trzy klasyczne prawa energii.
Prawo Rittingera zakłada, że zapotrzebowanie na energię jest proporcjonalne do nowo utworzonej powierzchni. Nadaje się ono szczególnie do rozdrabniania drobnego i bardzo drobnego. Specyficzne zużycie energii wynosi
Eₛ = KR · (1/d₂ − 1/d₁)
- d1: charakterystyczna wielkość ziarna wyjściowego, d2d_2d2: wielkość ziarna końcowego (np. d80 lub d50)
- KR: stała materiałowa/procesowa
Prawo Kicka opisuje zużycie energii jako funkcję stopnia rozdrobnienia. Nadaje się ono przede wszystkim do rozdrabniania grubego. Zakłada się geometryczne podobieństwo cząstek. Zużycie energii wynosi
Eₛ = KK · ln (d₁/d₂)
Prawo Bonda stosuje się w przypadku średnich stopni rozdrobnienia. Stanowi ono praktyczny kompromis między obydwoma podejściami i jest często stosowane w zakresie średniego rozdrobnienia. Uwzględnia ono fakt, że zapotrzebowanie na energię jest związane z pierwiastkiem kwadratowym wielkości ziarna. Zużycie energii wynosi
Eₛ = KB · (1/√d₂ − 1/√d₁)
- d1 jest charakterystyczną wielkością ziarna materiału wsadowego
- d2 jest charakterystyczną wielkością ziarna produktu mielonego
W praktyce przemysłowej prawo Bonda jest często stosowane w postaci wskaźnika pracy Bonda. W tym przypadku stosuje się charakterystyczne wielkości ziarna, takie jak 80% przejście wsadu F₈₀ i produktu P₈₀. Powszechnie stosowane równanie Bonda brzmi
Es = 10 · Wi · (1 / √P80 − 1 / √F80)
- F80: wielkość ziarna, przy której 80% wsadu jest drobniejsze
- P80: wielkość ziarna, przy której 80% produktu jest drobniejsze
- Es w kWh/t
- Wi = wskaźnik pracy Bonda (stała specyficzna dla materiału)
- F80, P80 w µm
Jednak nanoproszki mogą mieć również niepożądane skutki. Zużycie opon lub mikrocząsteczki tworzyw sztucznych mogą powodować zanieczyszczenie powietrza i wody pitnej. Mechanizmy obronne organizmu mogą tylko w ograniczonym stopniu chronić przed substancjami obcymi, jeśli występują one w postaci nanocząsteczek lub nanostruktur.

