Czynniki wpływające na efektywne nawilżanie proszku w procesie mieszania
W wielu gałęziach przemysłu materiały sypkie są rutynowo zwilżane różnymi cieczami. Na pierwszy rzut oka zwilżanie powierzchni stałej cieczą wydaje się banalne, na przykład gdy deszcz pada na ziemię lub gdy rozgrzana część kuta jest schładzana w wodzie. Zwilżanie substancji stałych w postaci proszku jest jednak znacznie bardziej złożone:
- Proszki mają bardzo dużą powierzchnię właściwą.
- Charakteryzują się wyraźną strukturą kapilarną.
- Ponadto mają różne (niejednorodne) powierzchnie cząstek.
Czynniki te determinują szybkość zwilżania i penetrację porów. W praktyce często prowadzi to do niepożądanych efektów:
- Powstają niepożądane aglomeraty lub grudki
- Płyn nie rozprowadza się równomiernie w zbiorze cząstek
- Zwilżony proszek ma złe właściwości płynięcia
- W mieszalniku dochodzi do przywierania, co zakłóca proces
Problemy tego typu można zazwyczaj dobrze rozwiązać za pomocą mieszalników amixon®. W trudniejszych przypadkach pomocne może być jednak zapoznanie się z niektórymi zależnościami fizycznymi.
Zwilżanie proszku może prowadzić do niepożądanego zabrudzenia mieszalnika
W zależności od lepkości i skłonności płynu do przywierania, na ściankach i narzędziach mieszających mogą tworzyć się osady. Wysoki stopień wypełnienia komory mieszania przeciwdziała temu zjawisku, ponieważ suchy proszek pełni rolę medium absorpcyjnego. Korzystne jest rozpylanie cieczy w dolnej części komory mieszania.
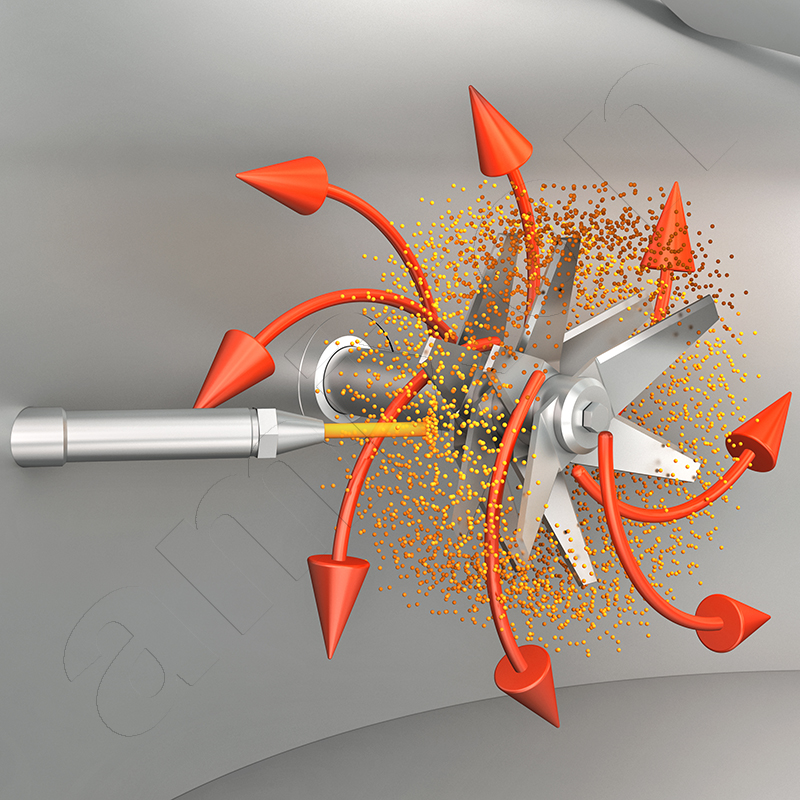
Decydujące znaczenie dla uniknięcia osadzania się pozostałości ma rodzaj wprowadzanej cieczy. Należy unikać wysokich gradientów stężenia. Z tego powodu amixon® stosuje lance natryskowe z odpowiednimi dyszami. Przepływ objętościowy cieczy zależy od zdolności adsorpcyjnej proszku i intensywności mieszania. Wyższa prędkość względna między kroplami a strumieniem cząstek sprzyja drobnemu rozproszeniu. Efekt ten można opisać za pomocą liczby Webera.
We = ρ v² d / γ
ρ … gęstość cieczy
v … prędkość względna kropli względem proszku
d … charakterystyczna średnica kropli
γ … napięcie powierzchniowe
Liczba Webera określa stosunek sił bezwładności kropli do stabilizujących sił powierzchniowych. Wysokie wartości sprzyjają rozpadowi kropli, a tym samym bardziej równomiernemu rozkładowi w proszku. Niskie wartości sprzyjają natomiast powstawaniu dużych kropli, które mają tendencję do przywierania do ścianek lub narzędzi mieszających.
Przywieranie w mieszalniku jest niepożądane. Może to zafałszować wynik mieszania. Ponadto przywierające cząstki mają tendencję do namnażania się z partii na partię i w niektórych przypadkach do niekontrolowanego odrywania się. Zanieczyszczenia zwiększają tarcie w procesie mieszania, powodują lokalne nagrzewanie się i w skrajnych przypadkach mogą blokować narzędzia. Optymalną metodę wprowadzania cieczy można określić w centrum technicznym amixon® w warunkach zbliżonych do praktycznych.
W zależności od lepkości i skłonności płynu do przywierania, na ściankach i narzędziach mieszających mogą tworzyć się osady. Wysoki stopień wypełnienia komory mieszania przeciwdziała temu zjawisku, ponieważ suchy proszek pełni rolę medium absorpcyjnego. Korzystne jest rozpylanie cieczy w dolnej części komory mieszania.
Decydujące znaczenie dla uniknięcia osadzania się pozostałości ma rodzaj wprowadzanej cieczy. Należy unikać wysokich gradientów stężenia. Z tego powodu amixon® stosuje lance natryskowe z odpowiednimi dyszami. Przepływ objętościowy cieczy zależy od zdolności adsorpcyjnej proszku i intensywności mieszania. Wyższa prędkość względna między kroplami a strumieniem cząstek sprzyja drobnemu rozproszeniu. Efekt ten można opisać za pomocą liczby Webera.
We = ρ v² d / γ
ρ … gęstość cieczy
v … prędkość względna kropli względem proszku
d … charakterystyczna średnica kropli
γ … napięcie powierzchniowe
Liczba Webera określa stosunek sił bezwładności kropli do stabilizujących sił powierzchniowych. Wysokie wartości sprzyjają rozpadowi kropli, a tym samym bardziej równomiernemu rozkładowi w proszku. Niskie wartości sprzyjają natomiast powstawaniu dużych kropli, które mają tendencję do przywierania do ścianek lub narzędzi mieszających.
Przywieranie w mieszalniku jest niepożądane. Może to zafałszować wynik mieszania. Ponadto przywierające cząstki mają tendencję do namnażania się z partii na partię i w niektórych przypadkach do niekontrolowanego odrywania się. Zanieczyszczenia zwiększają tarcie w procesie mieszania, powodują lokalne nagrzewanie się i w skrajnych przypadkach mogą blokować narzędzia. Optymalną metodę wprowadzania cieczy można określić w centrum technicznym amixon® w warunkach zbliżonych do praktycznych.
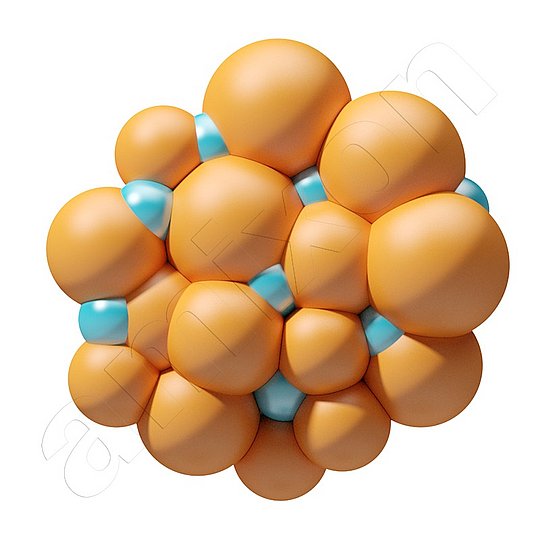
W jakim stopniu powierzchnia proszku przyciąga ciecze? Jak wygląda kapilarność proszku?
Afinitet proszku do cieczy zależy od energii powierzchniowej jego cząstek oraz od jego struktury kapilarnej. Obie te wielkości decydują o tym, jak łatwo ciecz się rozlewa lub cofa. Odpowiednią miarą fizyczną jest ciśnienie kapilarne. Opisuje ona siłę, z jaką ciecz jest wciągana do porów i przestrzeni międzycząsteczkowych proszku.
Δp = (2 γ cos θ) / r
Δp to ciśnienie kapilarne.
γ oznacza napięcie powierzchniowe cieczy.
θ to kąt zwilżania między cieczą a powierzchnią proszku.
r to efektywny promień kapilarny w proszku.
Wysokie napięcie powierzchniowe i mały kąt zwilżania powodują wysokie ciśnienie kapilarne. Dzięki temu ciecz jest szybko i głęboko wciągana do porów cząstek. Duże kąty zwilżania znacznie zmniejszają natomiast ciśnienie kapilarne. W tym przypadku ciecz pozostaje głównie na powierzchni cząstek. Małe promienie kapilarne zwiększają „efekt ssania” kapilary.
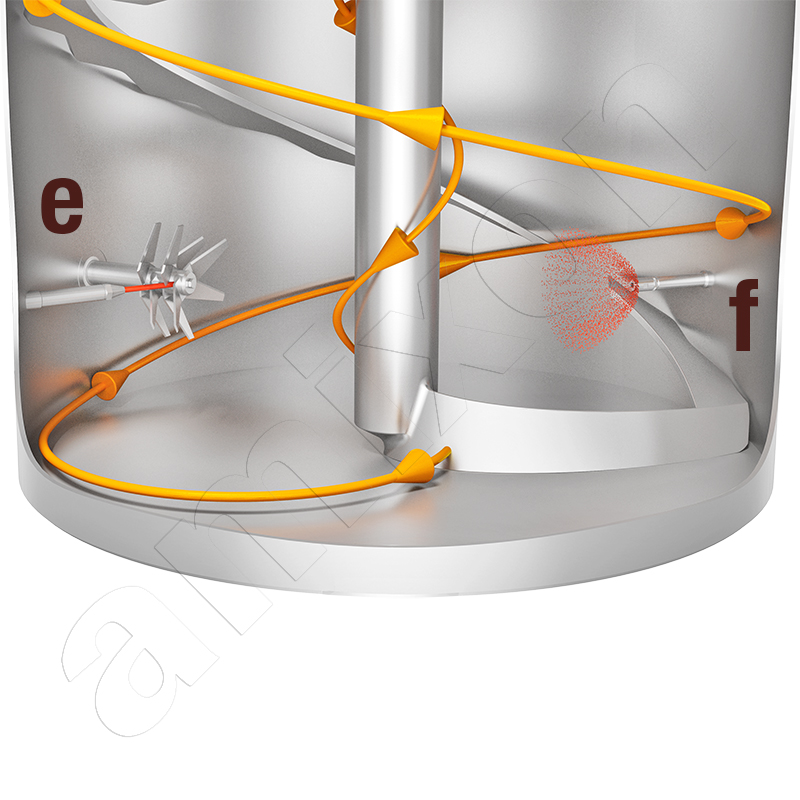
Objaśnienia do ilustracji:
a) Niskie napięcie powierzchniowe, b) Wysokie napięcie powierzchniowe, c) Ciecz cofająca się, d) Ciecz posuwająca się naprzód, e) Ciecz jest wtryskiwana do obszaru turbulencji wirnika (dysza jednoskładnikowa), f) Ciecz jest rozpylana w postaci mikrocząstek, a proszek ulega fluidyzacji (dysza dwuskładnikowa)
Afinitet proszku do cieczy zależy od energii powierzchniowej jego cząstek oraz od jego struktury kapilarnej. Obie te wielkości decydują o tym, jak łatwo ciecz się rozlewa lub cofa. Odpowiednią miarą fizyczną jest ciśnienie kapilarne. Opisuje ona siłę, z jaką ciecz jest wciągana do porów i przestrzeni międzycząsteczkowych proszku.
Δp = (2 γ cos θ) / r
Δp to ciśnienie kapilarne.
γ oznacza napięcie powierzchniowe cieczy.
θ to kąt zwilżania między cieczą a powierzchnią proszku.
r to efektywny promień kapilarny w proszku.
Wysokie napięcie powierzchniowe i mały kąt zwilżania powodują wysokie ciśnienie kapilarne. Dzięki temu ciecz jest szybko i głęboko wciągana do porów cząstek. Duże kąty zwilżania znacznie zmniejszają natomiast ciśnienie kapilarne. W tym przypadku ciecz pozostaje głównie na powierzchni cząstek. Małe promienie kapilarne zwiększają „efekt ssania” kapilary.
Objaśnienia do ilustracji:
a) Niskie napięcie powierzchniowe, b) Wysokie napięcie powierzchniowe, c) Ciecz cofająca się, d) Ciecz posuwająca się naprzód, e) Ciecz jest wtryskiwana do obszaru turbulencji wirnika (dysza jednoskładnikowa), f) Ciecz jest rozpylana w postaci mikrocząstek, a proszek ulega fluidyzacji (dysza dwuskładnikowa)
Kapilarność proszku i napięcie powierzchniowe cieczy
Struktura kapilarna proszku oraz napięcie powierzchniowe cieczy wpływają na łatwość, z jaką ciecz wnika w pory cząstek. Przy niskim napięciu powierzchniowym ciecz spontanicznie zwilża powierzchnię cząstek. Wnika również w drobne kapilary. W przypadku wysokiego napięcia powierzchniowego ciśnienie kapilarne jest natomiast niskie. Ciecz pozostaje na powierzchni i nie wypełnia porów w wystarczającym stopniu.
Dotyczy to zarówno pojedynczych cząstek, jak i pustych przestrzeni zbioru cząstek. W niniejszym przypadku równomierne rozprowadzenie cieczy jest zatem możliwe tylko wtedy, gdy proszek zostanie intensywnie wymieszany. Cząstki muszą być intensywnie ocierane o siebie.
Struktura kapilarna proszku oraz napięcie powierzchniowe cieczy wpływają na łatwość, z jaką ciecz wnika w pory cząstek. Przy niskim napięciu powierzchniowym ciecz spontanicznie zwilża powierzchnię cząstek. Wnika również w drobne kapilary. W przypadku wysokiego napięcia powierzchniowego ciśnienie kapilarne jest natomiast niskie. Ciecz pozostaje na powierzchni i nie wypełnia porów w wystarczającym stopniu.
Dotyczy to zarówno pojedynczych cząstek, jak i pustych przestrzeni zbioru cząstek. W niniejszym przypadku równomierne rozprowadzenie cieczy jest zatem możliwe tylko wtedy, gdy proszek zostanie intensywnie wymieszany. Cząstki muszą być intensywnie ocierane o siebie.
Jednorodne zwilżanie proszku nie jest sprawą trywialną
W stanie suchym cząstki są ściśle przylegające do siebie. Pomiędzy nimi znajduje się powietrze. Podczas mieszania przestrzenie te ulegają ciągłym zmianom. Po dodaniu cieczy powietrze musi zostać wyparte z porów. Najpierw ciecz tworzy cienką warstwę adsorpcyjną wokół cząstek. Warstwa ta jest zazwyczaj mocno przylegająca i można ją usunąć jedynie poprzez odparowanie.
Wraz ze wzrostem zawartości cieczy w miejscach styku powstają mostki kapilarne. Może to powodować łączenie się cząstek. W ten sposób rozpoczyna się granulacja strukturalna. Wraz z dalszym dodawaniem cieczy wypełniają się większe przestrzenie. Gdy wszystkie kapilary są wypełnione, proszek jest nasycony. Następnie przechodzi on w zawiesinę. Wnikanie cieczy do kapilar można opisać równaniem Washburna.
L² = γ * r * t * cos(θ) / (2 * η)
L to głębokość wnikania
γ to napięcie powierzchniowe
θ to kąt zwilżania
η to lepkość
r to promień kapilarny
t to czas.
Mały kąt zwilżania i niska lepkość sprzyjają penetracji. Natomiast wysoka lepkość lub powierzchnie hydrofobowe ją hamują. Zwilżalność zależy od mikrostruktury cząstek. Chropowatość zmienia pozorny kąt zwilżania. Opisuje to zależność Wenzel:
cos(θW) = rf * cos(θ)
θW to pozorny kąt zwilżania na chropowatej powierzchni
rf to współczynnik chropowatości.
Powierzchnie niejednorodne wykazują inne zachowanie. Obowiązuje tu równanie Cassiego-Baxtera:
cos(θCB) = f₁ * cos(θ₁) + f₂ * cos(θ₂)
θCB to pozorny kąt zwilżania na powierzchni mieszanej
f₁ i f₂ to udziały powierzchni różnych typów
Przy niskim napięciu powierzchniowym i wysokim powinowactwie może wystąpić tzw. absorpcja błyskawiczna. W tym przypadku dostępna ciecz jest natychmiast i całkowicie wchłaniana. Może to mieć negatywny wpływ na jakość mieszania. W takich przypadkach ciecz powinna być rozpylana wolniej i szczególnie drobno. Jeśli dodawanie odbywa się poniżej poziomu materiału sypkiego, można również uniknąć tworzenia się kondensatu w komorze mieszania. Narzędzia mieszające i komora mieszania pozostają czyste. Każdy gram płynu jest rozprowadzany w proszku bez strat.
W stanie suchym cząstki są ściśle przylegające do siebie. Pomiędzy nimi znajduje się powietrze. Podczas mieszania przestrzenie te ulegają ciągłym zmianom. Po dodaniu cieczy powietrze musi zostać wyparte z porów. Najpierw ciecz tworzy cienką warstwę adsorpcyjną wokół cząstek. Warstwa ta jest zazwyczaj mocno przylegająca i można ją usunąć jedynie poprzez odparowanie.
Wraz ze wzrostem zawartości cieczy w miejscach styku powstają mostki kapilarne. Może to powodować łączenie się cząstek. W ten sposób rozpoczyna się granulacja strukturalna. Wraz z dalszym dodawaniem cieczy wypełniają się większe przestrzenie. Gdy wszystkie kapilary są wypełnione, proszek jest nasycony. Następnie przechodzi on w zawiesinę. Wnikanie cieczy do kapilar można opisać równaniem Washburna.
L² = γ * r * t * cos(θ) / (2 * η)
L to głębokość wnikania
γ to napięcie powierzchniowe
θ to kąt zwilżania
η to lepkość
r to promień kapilarny
t to czas.
Mały kąt zwilżania i niska lepkość sprzyjają penetracji. Natomiast wysoka lepkość lub powierzchnie hydrofobowe ją hamują. Zwilżalność zależy od mikrostruktury cząstek. Chropowatość zmienia pozorny kąt zwilżania. Opisuje to zależność Wenzel:
cos(θW) = rf * cos(θ)
θW to pozorny kąt zwilżania na chropowatej powierzchni
rf to współczynnik chropowatości.
Powierzchnie niejednorodne wykazują inne zachowanie. Obowiązuje tu równanie Cassiego-Baxtera:
cos(θCB) = f₁ * cos(θ₁) + f₂ * cos(θ₂)
θCB to pozorny kąt zwilżania na powierzchni mieszanej
f₁ i f₂ to udziały powierzchni różnych typów
Przy niskim napięciu powierzchniowym i wysokim powinowactwie może wystąpić tzw. absorpcja błyskawiczna. W tym przypadku dostępna ciecz jest natychmiast i całkowicie wchłaniana. Może to mieć negatywny wpływ na jakość mieszania. W takich przypadkach ciecz powinna być rozpylana wolniej i szczególnie drobno. Jeśli dodawanie odbywa się poniżej poziomu materiału sypkiego, można również uniknąć tworzenia się kondensatu w komorze mieszania. Narzędzia mieszające i komora mieszania pozostają czyste. Każdy gram płynu jest rozprowadzany w proszku bez strat.
Fizyczne podstawy przylegania i tworzenia się warstwy
Niestety w praktyce wiele parametrów materiałowych nie jest dostępnych. Ich eksperymentalne określenie jest pracochłonne. Niemniej jednak pomocna jest znajomość równania konwekcji Marangoniego. Warstwy cieczy poruszają się, gdy zmienia się lokalnie ich napięcie powierzchniowe. Nawet niewielkie różnice temperatury lub stężenia mogą spowodować tworzenie się warstwy.
Ma = ((dγ/dT) * L * ΔT) / (μ * α)
Ma to liczba Marangoniego
γ to napięcie powierzchniowe
ΔT to różnica temperatur
µ to lepkość dynamiczna
α to dyfuzyjność cieplna
L to długość charakterystyczna
Skłonność do przywierania wzrasta zwłaszcza wtedy, gdy podczas zwilżania powstają lokalne różnice temperatury lub stężenia. Decydujące znaczenie ma nie bezwzględny poziom temperatury, ale wielkość gradientu. Procesy mieszania prowadzone w niskiej temperaturze mają zatem działanie stabilizujące, ponieważ utrzymują wysoką lepkość i minimalizują prądy Marangoniego. Wysokie wartości Ma prowadzą do niestabilności warstw cieczy.
Kolejnym istotnym mechanizmem jest adhezja cienkich warstw cieczy. Model Johnsona-Kendalla-Robertsa opisuje siłę przyczepności między dwiema cząstkami.
F = (3/2) * π * R * W
F to siła przyczepności
R to efektywny promień krzywizny cząstek
W to specyficzna praca adhezji
Wysokie wartości W sprzyjają powstawaniu silnych przylegania. Krople przylegają wtedy szczególnie mocno do narzędzi mieszających lub ścianek.
Najlepiej jest unikać wysokich gradientów stężenia. Dlatego amixon® często stosuje dysze dwu- i trójskładnikowe. Można je stosować w środku złoża proszku. Fluidyzują one proszek w obszarze wylotu i rozpylają ciecz na mikrocząsteczki. Dzięki temu wolna ciecz jest natychmiast absorbowana przez cząstki. Unika się w ten sposób przylegania.
Szczególnie korzystne jest, gdy proszek nie nagrzewa się podczas procesu mieszania. Mieszalniki amixon® wspierają ten proces, ponieważ działają w oparciu o delikatny i energooszczędny mechanizm mieszania, który generuje jedynie niewielkie efekty ścinania i tarcia.
Niestety w praktyce wiele parametrów materiałowych nie jest dostępnych. Ich eksperymentalne określenie jest pracochłonne. Niemniej jednak pomocna jest znajomość równania konwekcji Marangoniego. Warstwy cieczy poruszają się, gdy zmienia się lokalnie ich napięcie powierzchniowe. Nawet niewielkie różnice temperatury lub stężenia mogą spowodować tworzenie się warstwy.
Ma = ((dγ/dT) * L * ΔT) / (μ * α)
Ma to liczba Marangoniego
γ to napięcie powierzchniowe
ΔT to różnica temperatur
µ to lepkość dynamiczna
α to dyfuzyjność cieplna
L to długość charakterystyczna
Skłonność do przywierania wzrasta zwłaszcza wtedy, gdy podczas zwilżania powstają lokalne różnice temperatury lub stężenia. Decydujące znaczenie ma nie bezwzględny poziom temperatury, ale wielkość gradientu. Procesy mieszania prowadzone w niskiej temperaturze mają zatem działanie stabilizujące, ponieważ utrzymują wysoką lepkość i minimalizują prądy Marangoniego. Wysokie wartości Ma prowadzą do niestabilności warstw cieczy.
Kolejnym istotnym mechanizmem jest adhezja cienkich warstw cieczy. Model Johnsona-Kendalla-Robertsa opisuje siłę przyczepności między dwiema cząstkami.
F = (3/2) * π * R * W
F to siła przyczepności
R to efektywny promień krzywizny cząstek
W to specyficzna praca adhezji
Wysokie wartości W sprzyjają powstawaniu silnych przylegania. Krople przylegają wtedy szczególnie mocno do narzędzi mieszających lub ścianek.
Najlepiej jest unikać wysokich gradientów stężenia. Dlatego amixon® często stosuje dysze dwu- i trójskładnikowe. Można je stosować w środku złoża proszku. Fluidyzują one proszek w obszarze wylotu i rozpylają ciecz na mikrocząsteczki. Dzięki temu wolna ciecz jest natychmiast absorbowana przez cząstki. Unika się w ten sposób przylegania.
Szczególnie korzystne jest, gdy proszek nie nagrzewa się podczas procesu mieszania. Mieszalniki amixon® wspierają ten proces, ponieważ działają w oparciu o delikatny i energooszczędny mechanizm mieszania, który generuje jedynie niewielkie efekty ścinania i tarcia.
Czy praktyczne testy w mieszalniku są nadal aktualne?
Tak, ponieważ mimo że obecnie potrafimy precyzyjnie scharakteryzować proszki i ciecze, mieszanki proszkowe i procesy zwilżania pozostają złożone. Układy dyspersyjne są wrażliwe na wahania składu surowców. Podczas gdy procesy mieszania cieczy można obecnie dobrze symulować, w przypadku układów dyspersyjnych jest to rzadko możliwe.
Próby mieszania pokazują również nieoczekiwane efekty w praktyce. Procesy wieloetapowe są na przykład szczególnie interesujące przy przygotowywaniu mieszanek przypraw, napojów instant lub dietetycznych środków odżywczych.
W centrum technicznym amixon® niemal codziennie realizujemy najróżniejsze procesy zwilżania. Na podstawie Państwa oryginalnych produktów chętnie pokażemy Państwu, jak zachowują się Państwa proszki, jak wyglądają, jak płyną i czy się przyklejają. Praktyczne testy dostarczają wiarygodnych wyników, które można wykorzystać do wiarygodnych prognoz. Dlatego pozostają one nieodzowne.
Tak, ponieważ mimo że obecnie potrafimy precyzyjnie scharakteryzować proszki i ciecze, mieszanki proszkowe i procesy zwilżania pozostają złożone. Układy dyspersyjne są wrażliwe na wahania składu surowców. Podczas gdy procesy mieszania cieczy można obecnie dobrze symulować, w przypadku układów dyspersyjnych jest to rzadko możliwe.
Próby mieszania pokazują również nieoczekiwane efekty w praktyce. Procesy wieloetapowe są na przykład szczególnie interesujące przy przygotowywaniu mieszanek przypraw, napojów instant lub dietetycznych środków odżywczych.
W centrum technicznym amixon® niemal codziennie realizujemy najróżniejsze procesy zwilżania. Na podstawie Państwa oryginalnych produktów chętnie pokażemy Państwu, jak zachowują się Państwa proszki, jak wyglądają, jak płyną i czy się przyklejają. Praktyczne testy dostarczają wiarygodnych wyników, które można wykorzystać do wiarygodnych prognoz. Dlatego pozostają one nieodzowne.
© Copyright by amixon GmbH