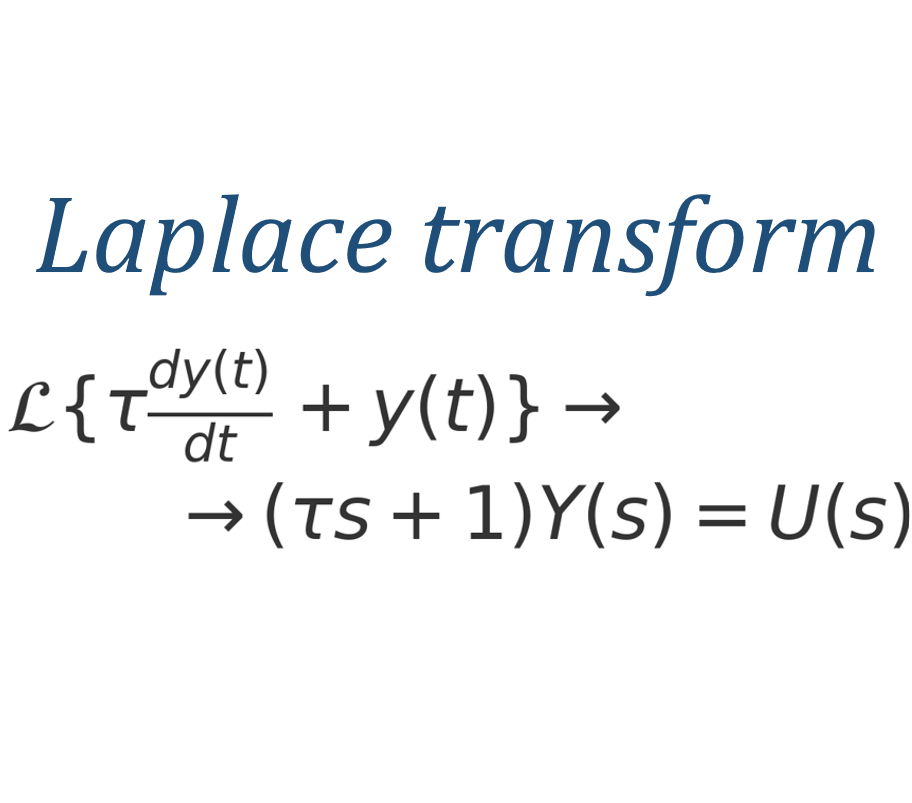라플라스 변환을 이용한 혼합 품질의 고장 분석

amixon® AMK 1000 믹서에서 연속 혼합 공정에 대한 라플라스 변환의 예시적 적용: 분말 A는 1,000 kg/h의 속도로 지속적으로 믹서로 유입됩니다. 분말 B는 동시에 10 kg/h로 계량됩니다. 혼합실은 시작 시 닫힌 상태로 유지됩니다. 혼합 도구는 이미 작동 중이며 20회 회전 후 이상적인 혼합 품질에 도달합니다. 회전 속도는 20 U/min입니다.

믹서에 700kg의 제품이 채워지면 배출 밸브가 열립니다. 유출량은 유입되는 1,010kg/h가 모두 배출되도록 설정됩니다. 공정은 안정적으로 진행됩니다.

갑작스러운 장애가 발생합니다: 성분 B의 공급이 20초 동안 완전히 중단됩니다. 이후 계량기가 보정되고 B는 20초 동안 두 배의 양(20 kg/h)으로 유입됩니다. 이후 유입량은 다시 10 kg/h로 안정화됩니다.

고장 발생 전에는 기술적으로 이상적인 혼합 품질이 유지되고 있었습니다. 혼합 품질의 변동 계수는 3%였습니다.

프로세스 현황 (초기 상황)

유입 A: ṁ_A = 1000 kg/h; 유입 B (명목): ṁ_B = 10 kg/h; 총 유입량: ṁ_ein = 1010 kg/h. 혼합기 내 분말 질량 상수: M = 700 kg.

평균 체류 시간 τ (시간 상수):

t = M / ṁ_aus = 700 / 1010 h = 0.693 h = 41.6 min = 2495 s

유입부(및 유출부에서 정상 상태)에서의 B의 명목 질량 비율:

x_B,in,0 = 10 / 1010 = 0.00990099 (≈ 0.9901 %)

장애 시나리오 (유입 B)

0 ≤ t < 20 s: 차단, ṁ_B = 0; 20 ≤ t < 40 s:

수정, ṁ_B = 20 kg/h; t ≥ 40 s: 다시 10 kg/h.

우리는 유입수에서 B 성분의 편차를 명목 분율에 대해 상대적으로 고려합니다:

u(t) = x_B,in(t) − x_B,in,0.

부분별 정의 (총 유량 근사값으로 일정 1010 kg/h):

u(t) = {-x_B,in,0 for 0≤t<20 s; +x_B,in,0 for 20≤t<40 s; 0 for t≥40 s}

동적 모델 (PT1, 이상적으로 혼합됨)

배출 비율 y(t) (배출구에서의 B 분획 편차)는 PT1 모델을 따릅니다:

dy(t)/dt + y(t) = u(t), y(0⁻) = 0

라플라스 해

PT1의 라플라스 변환:

Y(s) = (1 / (τ s + 1)) · U(s)

τ (타우): 시스템의 시간 상수 (여기서는 혼합기 내 평균 체류 시간)
s: 라플라스 변수, 신호가 시간에 따라 어떻게 변화하는지를 나타내는 척도
"τ · s"는 시간 상수와 변화율의 무차원 조합이다.

입력 u(t)는 두 사각형 도약의 차이로 표현되며, 헤비사이드 이동을 적용하면 다음과 같이 구해집니다:

U(s) = x_B,in,0 · (-1 + 2 e^{-20 s} - e^{-40 s}) / s

시간 영역 해법 (계단 응답의 중첩, Heaviside H(·)):

y(t)=x_B,in,0[ - (1 - e^{-t/τ}) H(t) + 2 (1 - e^{-(t-20)/τ}) H(t-20) - (1 - e^{-(t-40)/τ}) H(t-40) ]

수치값과 최대 편차

τ = 2495 s 및 x_B,in,0 = 0.00990099일 때 다음과 같이 계산됩니다:

e^{-20/τ} = e^{-20/2495} ≈ 0.99202; 1 - e^{-20/τ} ≈ 0.00798

차단 종료 시점(t = 20초)의 최대 음의 편차:

y(20) = - x_B,in,0 (1 - e^{-20/τ}) ≈ -7.9·10^{-5} (≈ -0.0079 % 절대값)

과다 투여 종료 시점 (t = 40초):

y(40) ≈ +6.3×10⁻⁷ (실질적으로 명목값)

t > 40초일 때, 미세한 잔여 편차는 지수적으로 감소한다:

y(t) = y(40) · e⁻^(t-40)/τ

혼합 품질 분류 (CV = 3 %)

장애로 인한 B 분획의 동적 편차(~0.8% 상대)는 혼합 품질의 변동계수(3%)보다 현저히 낮습니다. 따라서 제품 흐름에서 장애는 실질적으로 거의 관찰되지 않습니다.

라플라스 분석의 이점

라플라스 표현은 유입 프로파일이 배출 혼합 품질에 미치는 시간적 영향에 대한 폐쇄형 공식을 제공합니다. 이를 통해 최대 편차, 회복 시간 및 체류 시간의 영향을 신속하게 추정할 수 있어 혼합실 설계 및 보정 전략 수립에 유용합니다.

질량 흐름이 두 배로 증가하면 혼합 품질은 어떻게 변합니까?

질량 유량이 두 배로 증가하고 평균 체류 시간이 41.6분에서 20.8분으로 단축되면 혼합 품질 결과는 어떻게 변합니까? 분말 A는 1,000 kg/h 대신 2,000 kg/h로 유동합니다. 분말 B는 10 kg/h 대신 20 kg/h로 유동합니다. 동일한 연속식 혼합기 AMK 1000을 사용하며, 회전 주파수는 20 rpm, 충전량은 700kg이며, 구성 요소 A와 B도 동일합니다. 장애는 동일합니다: 구성 요소 A는 지속적으로 유입되고, 구성 요소 B는 20초 동안 차단된 후, 20초 동안 두 배의 양으로 유입됩니다. 이후 성분들은 규정대로 유동합니다.

결론

출구에서의 상대적 장애 편차는 이제 약 1.6%입니다(이전 0.8%). 체류 시간이 절반으로 줄어들었기 때문에 시스템은 두 배 빠르게 반응하며 약 두 배 큰 진폭 편차를 보입니다. 명목 분율은 변하지 않으므로, 효과는 1 - e^{-20/τ}로 직접 비례합니다.

혼합 품질에 대한 분류 (CV = 3 %)

1.6%의 상대적 동적 편차도 혼합 품질의 변동 계수(3%)보다 낮습니다. 제품 흐름에서 장애는 적당한 수준을 유지하지만, 첫 번째 사례보다 눈에 띄게 더 강합니다.

동적 편차가 3%일 때 어떤 일이 발생합니까?

동적 편차가 3%(1.6% 대신)로 “기본 분산”(CV = 3%) 수준에 도달하면 어떻게 될까요? 큰 장애로 인해 상대적 동적 편차가 1.6%가 아닌 3%가 된다면 혼합 품질의 변화를 어떻게 평가해야 할까요? 장애가 없는 운영과 유사하게 평가해야 할까요?

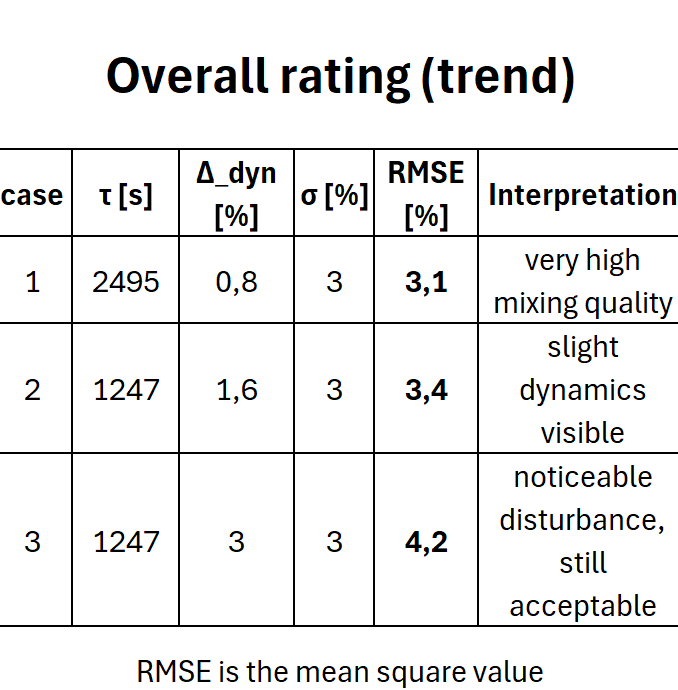
동적 편차는 이제 정적 CV의 규모에 해당합니다.
총 편차는 4% 이상으로 증가합니다.
품질은 대부분 ±5% 이내로 유지되지만, 이상치 발생 위험이 크게 증가합니다.

연속 혼합기는 저역 통과 필터처럼 작용합니다. 체류 시간을 절반으로 줄이면 동적 장애 편차가 약 두 배로 증가합니다. 이 편차가 변동 계수보다 낮을 때는 공정이 안정적으로 유지됩니다. 변동 계수와 같거나 더 커지면 편차가 분산에 제곱으로 더해집니다. 혼합 품질이 눈에 띄게 저하되지만 당분간은 통제 가능한 수준을 유지합니다.

혼합기