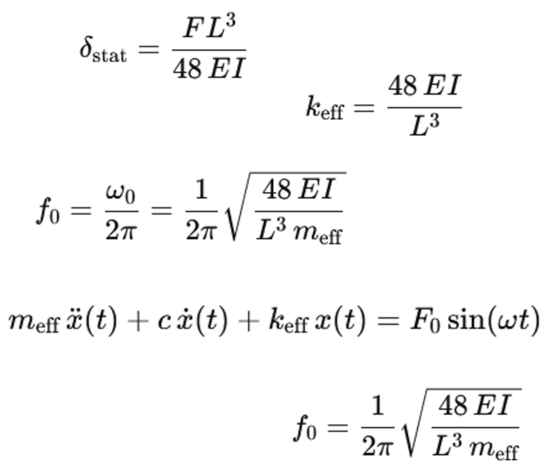Определение резонансных частот

Речь идет о первоначальной оценке вероятности того, что в данном случае речь идет о проблеме вибрации с риском резонанса. Следующее рассуждение относится к кольцевому гранулятору amixon®. Ситуация сильно идеализирована.

Кольцевой смесительный гранулятор установлен по центру на опорной конструкции с одним подшипником. Он рассматривается как точечная нагрузка. Он располагается справа и слева, как мост, на двух опорах. Машина имеет приводной двигатель и вращающийся вал смесителя. Двигатель и вал вращаются со скоростью n [оборотов в минуту]. Вал смесителя имеет небольшой дисбаланс. Это создает периодическую вертикальную силу в центре опоры. Для оценки система моделируется как одномассовый колебательный механизм. Опора рассматривается как пружина с жесткостью keff. Машина и часть опоры рассматриваются как эффективная масса m_(eff). Неуравновешенность создает гармоническую возбуждающую силу F(t). Необходимо оценить следующие данные:•

частота возбуждения
эффекты дисбаланса
теоретическая жесткость пружины
Собственная частота всей системы

Частота возбуждения дисбаланса

Частота вращения n выражается в оборотах в минуту. По частоте вращения рассчитывается частота возбуждения в герцах. Частота возбуждения fErreger в герцах равна: f_Erreger = n / 60. Частота возбуждения ω равна:

ω = 2 * π * f_Erreger = 2 * π * n / 60

ω = 2 π n/60

Пример: при n = 600 оборотов в минуту получается f_возбудитель = 10 герц.

В грануляторе с кольцевым слоем смесительная камера открывается.

Эффекты дисбаланса и сила дисбаланса

Несбалансированность описывается массой несбалансированности mu. Масса несбалансированности mu находится на расстоянии e от оси вращения. При вращении на несбалансированность действует центростремительная сила. Амплитуда силы несбалансированности F0 равна:

F₀= m_ue ω²

Временная сила возбуждения F(t) может быть принята за синусоидальную. Сила возбуждения тогда записывается как:

F(t) = F₀ sin (ω t)

Эта сила действует вертикально в центре балки.

Теоретическая жесткость пружины опоры в центре поля

Балка рассматривается как просто подпертая балка с точечной нагрузкой в середине. Пролет балки равен L. Жесткость балки на изгиб определяется произведением E * I. E — модуль упругости стали. I — момент инерции сечения. Статическая вертикальная сила F действует в середине балки. Статическая прогиб δ_stat в середине балки равен:

δ_stat = F L³/ (48 E I)

Жесткость пружины k_eff определяется как отношение силы к смещению. Применяя это, получаем:

k_eff = F / δ_stat = 48 E I / L³

Жесткость пружины k_eff описывает вертикальную жесткость балки в середине поля.

Кольцевой смесительный гранулятор.

Эффективная масса m_eff системы

Колеблющаяся масса состоит из массы машины и части массы опоры. Масса машины равна m_M. Масса опоры равна m_B. Не все части опоры колеблются с одинаковой силой. Поэтому используется коэффициент участия η. Коэффициент участия часто составляет от 0,2 до 0,3. Часто используется упрощенное значение η = 0,25. Эффективная масса m_eff затем рассчитывается как сумма:

m_eff= m_M+ η m_B

Если масса машины значительно превышает массу носителя, можно приблизительно установить m_eff ≈ m_M.

Собственная частота всей системы

Система рассматривается как одномассовый осциллятор с массой m_eff и жесткостью пружины k_eff. Дифференциальное уравнение неослабленного одномассового осциллятора имеет вид:

m_eff x¨(t) + k_eff x(t) = 0

Собственная частота ω_0 равна:

ω₀ = sqrt (k_eff/m_eff)

Собственная частота f_0 в герцах равна:

f₀ = ω₀/ (2π)

f₀ = (1 / (2 π)) sqrt (k_eff / m_eff)

Если заменить k_eff на 48 * E * I / L^3, получится:

f₀ = (1 / (2 π)) sqrt ((48 E I) / (L³ m_eff))

Эта формула показывает, что собственная частота увеличивается с увеличением жесткости на изгиб E * I и уменьшается с увеличением размаха L и эффективной массы m_eff.

Сравнение частоты возбуждения и собственной частоты для оценки опасности резонанса

Частота возбудителя f_Erreger рассчитывается на основе частоты вращения машины. Собственная частота f_0 рассчитывается на основе жесткости подшипника и эффективной массы. Опасность резонанса возникает, когда частота возбудителя близка к собственной частоте. Условие резонанса приблизительно выглядит следующим образом:

f_Erreger ≈ f₀

Для обеспечения безопасности конструкции необходимо соблюдать расстояние между собственной частотой и частотой возбуждения. Часто в качестве ориентировочного значения выбирается разница примерно в 20 процентов или более. Если собственная частота значительно превышает весь диапазон скоростей, вероятность резонанса невелика. Если собственная частота значительно ниже всего диапазона скоростей, вероятность резонанса также невелика. Если собственная частота находится в пределах используемого диапазона скоростей, вероятно возникновение проблемы с вибрацией.

Это выведение позволяет сделать первоначальную оценку того, следует ли ожидать возникновения проблемы резонанса в кольцевом смесительном агломераторе на носителе.

Это рассуждение позволяет сделать первоначальную оценку, чтобы понять, следует ли ожидать возникновения проблемы резонанса в кольцевом смесителе-агломераторе на опоре.

Back